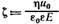Лекция №4
К межфазным взаимодействиям между конденсированными фазами относятся смачивание, растекание и адгезия.
Как правило, адгезия и смачивание сопровождают друг друга. Эти явления широко распространены в природе и в различных отраслях промышленности (нанесение лакокрасочных покрытий, получение материалов на основе связующих и наполнителей — бетон, резина и т. д.)
АДГЕЗИЯ
Адгезия — межфазное взаимодействие, или взаимодействие между приведёнными в контакт поверхностями конденсированных тел разной природы (прилипание). Адгезия обеспечивает между двумя телами соединение определенной прочности, обусловленное межмолекулярными силами.
Адгезия — результат стремления системы к уменьшению поверхностной энергии, поэтому это самопроизвольный процесс. Работа адгезии Wa, характеризующая прочность адгезионной связи, определяется работой обратного разрыва адгезионной связи, отнесённой к единице площади:
W s = WаS, где Ws — полная работа адгезии (4.1)
Cоотношение между Wa и s :
Предположим, что имеется контакт между 3 фазами — 1 — газ, 2 -жидкость, 3 — твердое тело, 2, 3 — конденсированные фазы. Введем следующие обозначения поверхностных натяжений:
s 2,3 — поверхностное натяжение на границе раздела двух конденсированных фаз
s 2,1 и s 3,1 — поверхностное натяжение на границе с воздухом
Уравнение Дюпре отражает закон сохранения энергии при адгезии. Из него следует, что работа адгезии тем больше, чем больше поверхностные натяжения исходных компонентов и чем меньше конечное межфазное натяжение.
Уравнение 4.2 справедливо только для изобарно-изотермического процесса в отсутствии электрического и химического взаимодействия между контактирующими телами, его используют только для определения равновесной работы адгезии жидкости.
Равновесную работу адгезии можно сопоставить с равновесной работой когезии. Когезия — определяет связь между молекулами внутри тела и в пределах одной фазы, характеризует прочность конденсированных тел и их способность противодействовать внешнему усилию.
Механизм адгезии
Первая стадия — транспортная, перемещение адгезива (клеящего вещества) к поверхности субстрата (тело, на которое наносят адгезив) и их определенное ориентирование в межфазном слое.
Вторая стадия — взаимодействие адгезива и субстрата, обусловлено различными силами (от ван-дер-ваальсовых до химических).
Завершается процесс адгезии межмолекулярным взаимодействием контактирующих фаз, что соответствует минимальной поверхностной энергии. Различают несколько механизмов (и, соответственно, теорий) в зависимости от природы взаимодействующих тел и условий, при которых происходит адгезия.
1.Механическая адгезия — осуществляется путем затекания в поры и трещины поверхности твердого тела жидкого адгезива., который потом затвердевает, обеспечивая механическое зацепление.
2.Молекулярная (адсорбционная) адгезия — возникает под действием межмолекулярных ван-дер-ваальсовых сил и водородных связей.
3.Электрическая теория — связана с образованием ДЭС на границе раздела между адгезивом и субстратом.
4.Диффузионный механизм — предусматривает взаимное проникновение молекул и атомов в поверхностные слои взаимодействующих фаз.
Чаще всего механизм адгезии является смешанным.
Теоретическая оценка адгезии очень приближённа, т. е., механизм её недостаточно изучен.
СМАЧИВАНИЕ
Смачивание — это поверхностное явление, заключающееся во взаимодействии жидкости с твёрдым или другим жидким телом при наличии контакта трех несмачивающихся фаз, одна из которых воздух.
Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания) или просто краевым углом (углом смачивания).
Рис.4.2. К выводу уравнения для краевого угла (закон Юнга).
Рис.4.2. иллюстрирует состояние капли жидкости на поверхности твердого тела в условиях равновесия. Поверхностная энергия твердого тела, стремясь уменьшиться, вызывает растяжение капли по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с воздухом s 3,1 .Межфазная энергия на границе твердого тела с жидкостью s 2,3 стремится сжать каплю. Растеканию препятствуют когезионные силы, действующие внутри капли. Действие когезионных сил направлено от границы между твердой, жидкой и газообразной фазами по касательной к сферической поверхности капли и равно s 2,1 .Угол q — краевой угол или угол смачивания.
Чем меньше краевой угол , тем лучше смачивание поверхности.
Если cos( q )>0 , то поверхность хорошо смачиваемая, cos( q )
Если разность s 3,1 — s 2,3 в уравнении Дюпре заменить её выражением из закона Юнга, то
Wa/ s 2,1 = 1+ cos( q ) — уравнение Дюпре-Юнга (4.5)
4.3, 4.4, 4.5 — только для идеально гладких тел. На поверхности реальных тел есть поры, трещины, и т. д.
Рассмотрим кинетический катерезис, который замедляет достижение равновесной формы капли.
Рис.4.3.Статические углы натекания и оттекания.
Для реальных тел: равновесный угол смачивания равен полусумме предельных углов натекания и оттекания:
cos( q ) = (cos( q нт ) + сos( q от ))/2 (4.6)
Влияние шероховатости на кривой угол:
k = cos( q ш )/cos( q ) , где к — коэфф. шероховатости
При повышении степени шероховатости смачиваемость улучшается.
РАСТЕКАНИЕ
Капля жидкости, нанесенная на поверхность, может оставаться на ее определенном участке, и система будет находится в равновесии в соответствии с законом Юнга, или же растекаться по поверхности. В обоих случаях система переходит в состояние с минимальной энергией Гиббса.
Из этого соотношения следует, что уменьшение межфазного натяжения s 2,3 (увеличение работы адгезии) и поверхностного натяжения жидкости s 2,1 , способствует растеканию жидкости.
Растекание происходит в том случае, если работа адгезии превышает работу когезии.
Способность жидкости растекаться зависит от когезии наносимых на поверхность жидкостей.
С повышением температуры увеличивается работа адгезии, поэтому нерастекающаяся жидкость с увеличением температуры может начать растекаться.
Источник
Экзаменационный билет № 4. 1. Адгезия и смачивание, определения
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием).
Работа адгезии Wа, характеризующая прочность адгезионной связи, определяется работой обратимого разрыва адгезионной связи, отнесенной к единице площади. Ома измеряется в тех же единицах, что и поверхностное натяжение (Дж/м 2 ). Полная работа адгезии, приходящаяся на всю площадь контакта тел s, равна
Чтобы получить соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхности на границе с воздухом 1, равные единице площади.
Для начального и конечного состояний системы имеем
Изменение энергии Гиббса системы в процесс адгезии равно
Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии.
Условие растворения:
Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).
Угол θ, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом, или углом смачивания.
Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:
Полученное соотношение называется законом Юнга.
Чем меньше угол Θ и соответственно больше cos θ, тем лучше смачивается поверхность. При остром угле Θ, т. е. при cos θ>0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол θ тупой, т. е. соs θ
Уравнение Дюпре самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга
Если разность в уравнении Дюпре заменить ее выражением нз закона Юнга
, получим
Это уравнение называют уравнением Дюпре-Юнга; оно связывает работу адгезии с краевым углом и позволяет рассчитать работу адгезии, если известны поверхностное натяжение жидкости и краевой угол. Обе эти величины можно сравнительно легко определить экспериментально.
Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.
2. Электрокинетические явления. Электростатический потенциал. Вывод уравнения Смолуховского для электроосмоса (или электрофореза). Эффекты, не учитываемые уравнением Смолуховского (поверхностная проводимость, элсктрофоретическое торможение, релаксационный эффект).
Протекание электрокинетических явлений в дисперсных систе-иах возможно при наличии на границе раздела фаз двойного электрического слоя, имеющего диффузное строение. При относительном перемещении фаз независимо от причин, его вызвавших, происходит разрыв двойного электрического слоя по плоскости скольжения.
Потенциал, возникающий на плоскости скольжения при отрыае части диффузного слоя, называется электрокинетическим потенциалом или ζ (дзета)-потенциалом.
Для получения наиболее простого уравнения, связывающего скорость относительного движения фаз с параметрами дисперсионной среды (вязкость, диэлектрическая проницаемость), двойного электрического слоя (ζ-потенциал) и внешнего электрического поля (напряженность), необходимо задаться некоторыми ограничениями:
1) толщина двойного электрического слоя значительно меньше радиуса пор, капилляров твердой фазы (радиуса кривизны поверхности твердой фазы);
2) слой жидкости, непосредственно прилегающий к твердой фазе, неподвижен, движение жидкости в порах твердой фазы ламинарное и подчиняется законам гидродинамики;
3) распределение зарядов в двойном электрическом слое не зависит от приложенной разности потенциалов;
4) твердая фаза является диэлектриком, а жидкость проводит электрический ток.
Электрическая сила, действующая на слой жидкости dх (в расчете на единицу площади поверхности), равна
Сила трения и ее дифференциал, приходящиеся на единиц) площади (согласно закону Ньютона), составляют:
При установившемся движении (в стационарном состоянии) dFэл = dFтр:
После интегрирования, окончательно получим следующее выражение для постоянной линейной скорости жидкости относительно мембраны:
Это уравнение носит название уравнения Гельмгольца — Смолуховского.
Уравнение Гельмгольца — Смолуховского чаще записывают относительно ζ-потенциала:
Это дифференциальное уравнение справедливо как для электроосмоса, так и для электрофореза, поскольку оно было выведено из баланса движущих сил процесса — электрической силы и силы трения. Отличие состоит только в выбранной системе координат.
Несовпадение экспериментальных и теоретических значений электрофоретнческой подвижности определяется в основном двумя эффектами, неучтенными теорией Гельмгольца — Смолуховского: релаксационным эффектом и электрофоретическим торможением.
Релаксационный эффект проявляется в нарушении симметрии диффузного слоя вокруг частицы при относительном движении фаз в противоположные стороны. Возникает внутреннее электрическое поле (диполь), направленное против внешнего поля. Для восстановления равновесного состояния системы требуется некоторое время, называемое временем релаксации.
Электрофоретическое торможение обусловлено сопротивлением движению частицы обратным потоком противоионов, который увлекает за собой жидкость. Вследствие этого электрофоретическая скорость уменьшается.
3. По результатам измерения адсорбции на активированном угле рассчитайте удельную поверхность адсорбента (величина адсорбции указана в расчете на азот при нормальных условиях):
| P·10 -2 , Па | А·10 3 , м 3 /кг |
| 1,85 | 5,06 |
| 4,01 | 9,90 |
| 68,80 | 40,83 |
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник