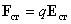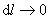- Электродвижущая сила
- Что такое электродвижущая сила — определение, физический смысл
- В чем измеряется в системе СИ, как обозначается на схеме
- Природа ЭДС, какими причинами порождается
- По какой формуле определяется электродвижущая сила
- Чему равна электродвижущая сила источника тока
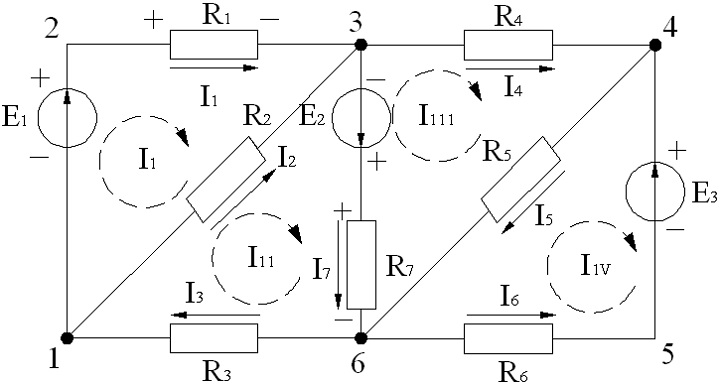
- 16. Электродвижущая сила.
- 17. Закон ома.
Электродвижущая сила
Что такое электродвижущая сила — определение, физический смысл
Электродвижущая сила (ЭДС) — физическая величина, описывающая работу любых сил, которые действуют в квазистационарных цепях постоянного или переменного тока, за исключением диссипативных и электростатических сил.
Для определения силы тока Георг Симон Ом использовал принцип крутильных весов Кулона. На длинной тонкой нити подвешено горизонтальное коромысло с заряженным шариком на конце. Второй заряд закреплен на cпицe, пропущенной сквозь крышку весов. При их взаимодействии коромысло поворачивается. Вращение головки в верхней части весов закручивало нить, возвращая коромысло в исходное состояние. По углу закручивания можно рассчитать силу взаимодействия зарядов в зависимости от расстояния между ними.
Ом по величине угла закрутки судил о силе тока I в проводнике, т. е. количестве электричества, перенесенном через поперечное сечение проводника за единицу времени. В качестве основной характеристики источника тока Ом брал величину напряжения \varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину \(\varepsilon\) он назвал электродвижущей силой, сокращенно ЭДС.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В чем измеряется в системе СИ, как обозначается на схеме
Электродвижущая сила в системе СИ измеряется в вольтах.
На схеме обозначение источника тока с ЭДС — две линии с плюсом и минусом, иногда круг.
Природа ЭДС, какими причинами порождается
Термопара — проволоки из разнородных металлов, соединенные концами.
Изучая термопары, немецкий физик Томас Иоганн Зеебек обнаружил в 1821 году следующую закономерность: когда точки соединения имеют разную температуру, в цепи возникает электродвижущая сила. Это явление назвали термоэлектрическим эффектом Зеебека. Величина такой электродвижущей силы зависит от температуры и неодинакова для разных пар металлов. Наиболее точных измерений Ом добился в 1826 году, использовав термопару из меди и висмута.
Внутри источника ЭДС электрический ток течет не от «плюса» к «минусу», а в противоположном направлении. Чтобы заставить ток двигаться в направлении, противоположном электростатической силе, которая воздействует на положительные заряды, необходимо приложить стороннюю силу: силу Лоренца, силу электрохимической природы, центробежную силу и т. п. Диссипативные силы не могут двигать электрические заряды против направления электростатической силы, поэтому к сторонним силам в данном случае не относятся.
По какой формуле определяется электродвижущая сила
В первых опытах Ом подключал к источнику тока проводники из разных материалов — серебра, меди, золота, — но одинакового сечения. Изменяя их длину l, Ом добивался, чтобы получалась одна и та же сила тока I. Обобщив результаты измерений, он вывел отношение:
Здесь \(R_i\) — некоторая постоянная, характеризующая внутреннее сопротивление гальванического элемента, а \(R(l)\) — величина, названная Омом сопротивлением проводника; она оказалась пропорциональна его длине, т. е. \(\;R(l)\;\sim\;l.\)
Из этой формулы следует, что найти электродвижущую силу можно, перемножив силу тока и полное сопротивление всей цепи:
Разность потенциалов на концах участка цепи равна падению напряжения на нем. Если в цепь включен источник тока, то ЭДС прибавляется к величине разности потенциалов или вычитается из нее в зависимости от полярности подключения. Когда на участке АВ имеется источник тока с ЭДС \(\varepsilon\) , разность потенциалов изменяется на величину \(\triangle U\;=\;\pm\;\varepsilon.\)
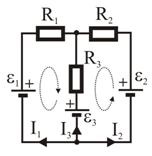
Знак выбирается в зависимости от полярности включения источника: по току или против него. Закон Ома в этом случае принимает вид:
При последовательном соединении источников полная электродвижущая сила цепи будет равняться сумме ЭДС отдельных источников. При параллельном соединении только источник с самой большой ЭДС будет источником, остальные окажутся потребителями.
Чему равна электродвижущая сила источника тока
ЭДС источника тока — это работа сторонних сил, нужная для перемещения единичного положительного заряда внутри источника от одного полюса к другому. Эту работу нельзя выразить через разность потенциалов, так как сторонние силы не имеют потенциала, их работа зависит от траектории.
При перемещении заряда между клеммами источника вне самого источника работа сторонних сил окажется нулевой.
Источник
16. Электродвижущая сила.
Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил.Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока.Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) , действующей в электрической цепи или на ее участке.
Представим стороннюю силу , действующую на заряд q, в виде
,
где векторная величина представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна
Интеграл, вычисленный для замкнутой цепи, дает ЭДС, действующую в этой цепи,
.
Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника. Физическая природа электродвижущих сил в разных источниках весьма различна.
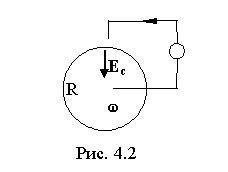
Рассмотрим пример. Пусть имеется металлический диск радиуса R (рис. 4.2), вращающийся с угловой скоростью 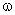


.
17. Закон ома.
Немецкий физик Г. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (отсутствуют сторонние силы)металлическому проводнику, пропорциональна падению напряжения на проводнике:
.
Сопротивление проводника. Величина R называется электрическим сопротивлением проводника. Единица сопротивления — 1 Ом. Для однородного цилиндрического проводника
где l — длина проводника; S — площадь его поперечного сечения; 


Обозначим их потенциалы 


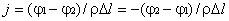
.
Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что
,
где Е — напряженность электрического поля внутри проводника. Учитывая, что j и Есовпадают по направлению, получаем
.
Это соотношение является дифференциальной формой закона Ома для однородного участка цепи. Величина 


.
От закона Ома в дифференциальной форме легко перейти к интегральной форме. Рассмотрим неоднородный участок цепи. Внутри этого участка выберем контур тока, удовлетворяющий следующим условиям: в каждом сечении, перпендикулярном к контуру, величины 



.
Умножим это соотношение на dl и проинтегрируем вдоль контура:
,
где 


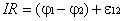



.
Последняя формула выражает закон Ома для неоднородного участка цепи. Для замкнутой цепи закон Ома имеет вид
,
где R — сопротивление нагрузки, r — внутреннее сопротивление источника тока.
Источник