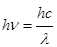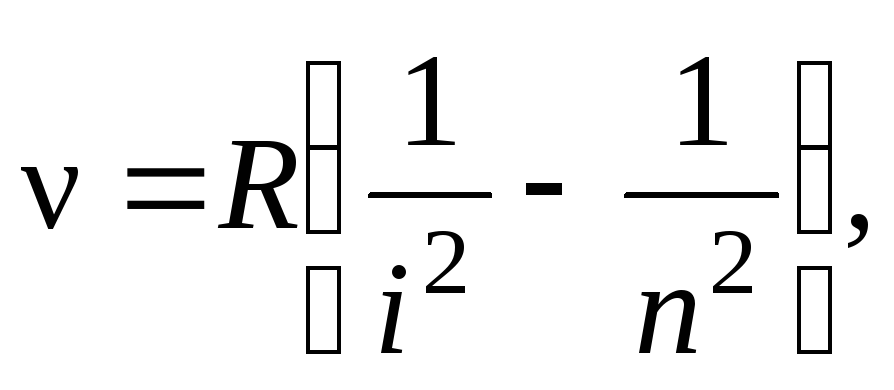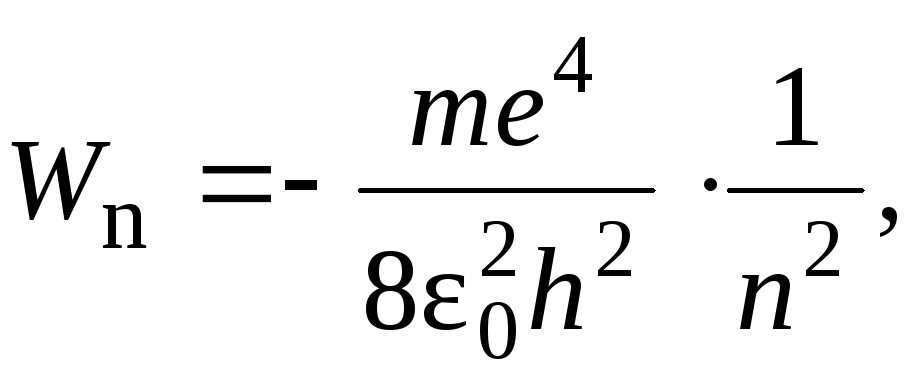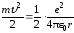Объясните природу линейчатых спектров

Виды спектров. Спектральный анализ.

Спектральный состав излучения атомов различных веществ весьма разнообразен. Тем не менее, все спектры можно разделить на три сильно отличающихся друг от друга типа.

Непрерывные (сплошные) спектры. В непрерывном спектре излучения (Рис 4.12.1) представлены волны всех длин. В спектре нет разрывов, и на экране спектрографа можно видеть сплошную разноцветную полосу с плавным переходом от одного цвета к другому.

Непрерывные (или сплошные) спектры дают тела, находящиеся в твердом или жидком состоянии, а также сильно сжатые газы. Для получения непрерывного спектра нужно нагреть тело до высокой температуры. Характер непрерывного спектра и сам факт его существования определяются не только свойствами отдельных излучающих атомов, но и в сильной степени зависят от взаимодействия атомов друг с другом. Непрерывный спектр дает также высокотемпературная плазма. Электромагнитные волны излучаются плазмой в основном при столкновении электронов с ионами.

Линейчатые спектры. Линейчатые спектры излучения (Рис 4.12.2,3,4) представляют собой набор цветных линий различной яркости, разделенных широкими темными полосами. Наличие линейчатого спектра означает, что вещество излучает свет только вполне определенных длин волн (точнее, в определенных очень узких спектральных интервалах). Каждая из линий имеет конечную ширину. Линейчатые спектры дают все вещества в газообразном атомарном (но не в молекулярном) состоянии. Изолированные атомы химического элемента излучают строго определенные длины волн, характерные данному химическому элементу. Природа линейчатых спектров объясняется тем, что у атомов конкретного вещества существуют только ему свойственные стационарные состояния со своим набором энергетических уровней.

Обычно для наблюдения линейчатых спектров используют свечение паров вещества в пламени или свечение газового разряда в трубке, наполненной исследуемым газом. При увеличении плотности атомарного газа отдельные спектральные линии расширяются и, при очень большой плотности газа, когда взаимодействие атомов становится существенным, эти линии перекрывают друг друга, образуя непрерывный спектр.

Полосатые спектры. Полосатые спектры излучения состоят из отдельных полос, разделенных темными промежутками (Рис 4.13: а, б). С помощью очень хорошего спектрального прибора можно обнаружить, что каждая полоса представляет собой совокупность большого числа очень тесно расположенных линий. В отличие от линейчатых спектров полосатые спектры создаются не атомами, а молекулами, не связанными или слабо связанными друг с другом.

Спектры поглощения. Если пропускать белый свет сквозь холодный, неизлучающий газ, то на фоне непрерывного спектра источника появляются темные линии поглощения (Рис. 4.14). Газ поглощает наиболее интенсивно свет как раз тех длин волн, которые он испускает в сильно нагретом состоянии. Темные линии на фоне непрерывного спектра — это линии поглощения, образующие в совокупности спектр поглощения. Спектры поглощения могут быть непрерывными, линейчатыми и полосатыми.

Атом, поглощая свет, переходит из основного состояния в возбужденное, причем для возбуждения атомов пригодны строго определенные кванты энергии , соответствующие данному газу. Поэтому газ поглощает из непрерывного спектра те самые кванты света, которые может излучать сам.

На рисунках 4.12 и 4.14 сопоставлены спектры испускания и поглощения разреженных паров натрия, водорода и гелия. Изучая спектры испускания и поглощения атомов, еще в 19 веке физики пришли к выводу, что атом не является неделимой частицей, а обладает некоторой внутренней сложной структурой.

Использование линейчатых спектров лежит в основе спектрального анализа – метода исследования химического состава веществ по их спектрам. Отдельные линии в спектрах различных элементов могут совпадать, но в целом спектр каждого элемента является его индивидуальной характеристикой. Спектральный анализ сыграл большую роль в науке. Например, в спектре Солнца (1814) были открыты фраунгоферовы темные линии, происхождение которых объясняется следующим образом. Солнце, являясь раскаленным газовым шаром (Т ~ 6000 °С), испускает сплошной спектр.

Солнечные лучи проходят через атмосферу Солнца (солнечную корону, температура которой ~2000-3000 °С. Корона поглощает из сплошного спектра излучение определенной частоты, а на Земле регистрируется солнечный спектр поглощения (рис. 4.14.5), по которому можно определить, какие химические элементы присутствуют в короне Солнца. По спектрам поглощения на Солнце были обнаружены все земные элементы, а также неизвестный ранее элемент, который назвали гелий. Через 26 лет (1894) открыли гелий на Земле. Благодаря спектральному анализу на Земле было открыто еще 25 химических элементов.

Более того, спектральный анализ Солнца и звезд показал, что входящие в их состав химические элементы имеются и на Земле, т.е. вещество Вселенной состоит из одного и того же набора элементов. Из-за своей сравнительной простоты и универсальности спектральный анализ является основным методом контроля состава вещества в металлургии и машиностроении. С помощью спектрального анализа определяют химический состав руд и минералов как по спектрам испускания, так и по спектрам поглощения. Состав сложных смесей анализируется по молекулярным спектрам. При определенных условиях методами спектрального анализа можно не только определить химический состав компонент, но и их количественное содержание.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Линейчатые спектры и закономерности в них

Изучая соотношение частот разных спектральных линий в видимой области спектра атома водорода, Бальмер вывел эмпирическую формулу, которая описывала наблюдаемые частоты и позволила предсказать ряд других, ранее не наблюдавшихся. Позднее другими исследователями были получены аналогичные соотношения для частот спектральных линий, входящих в другие области спектра водорода (ультрафиолетовую и инфракрасную). С учётом всех этих данных обобщённая формула Бальмера имеет вид:

(4)

где — частота, испускаемого света; i = 1, 2, 3, 4 — целое число, характеризующее серию линий; n = i +1, i + 2, . — целое число, характеризующее конкретную линию серии; R = 3,28·10 15 с –1 — постоянная Ридберга. При i = 1 описывается так называемая серия Лаймана в ультрафиолетовой области, при i = 2 — серия Бальмера в видимой области, при n = 3, 4, 5 — серии Пашена, Брэкета и Пфунда в инфракрасной области.

Простота формулы Бальмера и точность описания спектра предполагала, что эта формула не формальна, а имеет глубокий смысл, т.е. её можно получить теоретически. Бор рассмотрел атом водорода с учётом предложенных постулатов.

Боровская теория атома водорода

Электрон, двигаясь по круговой орбите радиусом r, обладает центростремительным ускорением a =  2 / r. Между электроном и ядром действует кулоновская сила притяжения F = e 2 /(4_r 2 ). По второму закону Ньютона запишется:

(5)

Здесь m и  — масса и скорость электрона; e — заряд электрона и ядра по абсолютной величине; ₀ — электрическая постоянная. Из второго постулата Бора  = nh/(2mr). Подставляя это значение в выражение (4), находим, что

(6)

Отсюда следует, что электрон движется лишь по орбитам вполне определённого, а не любого радиуса. При n = 1 получаем радиус первой боровской орбиты

r₁ = _h 2 /(me 2 ). (7)

Тогда радиусы остальных орбит определяются из соотношения

r = r₁n 2 . (8)

Формула (7) позволила оценить размеры атома водорода (~10 –10 м), который определяется радиусом вращения электрона.

Полная энергия W атома при движении электрона по орбите радиуса r складывается из кинетической энергии W_k электрона относительно ядра и потенциальной энергии W_p взаимодействия электрона с ядром, т.е. W = W_k + W_p. Уравнение (5) преобразуем к виду:

или W_k =  (1/2)W_p, (9)

поскольку W_p =  потенциальная энергия взаимодействия двух зарядов и m 2 /2 = W_k  кинетическая энергия электрона. Учитывая это и выражение (9), получаем, что W= (1/2)W_p = . Подставляя в эту формулу соотношение (6), находим:

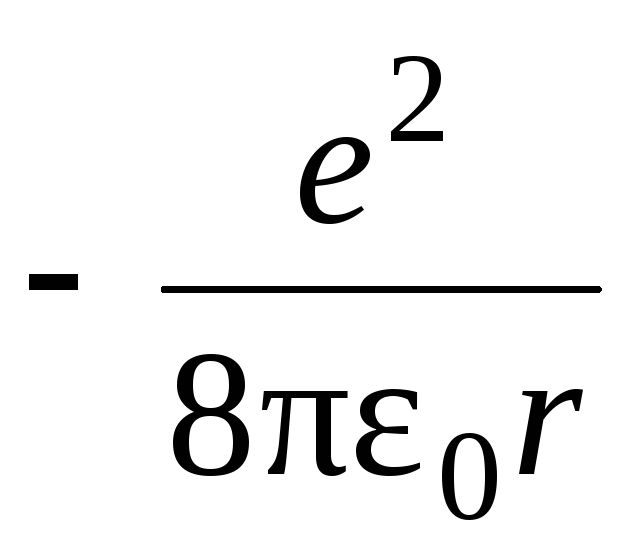
(10)

где n может принимать только целые значения 1, 2, 3, . . Величину n в квантовой физике называют главным квантовым числом.

На основе выше сказанного можно объяснить природу линейчатых спектров. Согласно третьему постулату Бора, энергия испущенного или поглощённого кванта с учётом (10) равна:

h = W_n  W_i = (11)

(12)

Сравнивая это выражение с соотношением (4), видим, что теоретическим путём была получена формула Бальмера. Постоянная Ридберга вычисленная по формуле и найденная экспериментально совпадают.

Таким образом, теория Бора позволила вычислить энергию атома водорода, его размеры и объяснить происхождение линейчатых спектров. Слабой стороной теории Бора была внутренняя логическая противоречивость: с одной стороны, она использовала классическую теорию (закон Ньютона), с другой  новые квантовые представления (постулаты Бора). После открытия волновых свойств вещества стало совершенно ясно, что теория Бора явилась только переходным этапом на пути создания новой последовательной теории атомных явлений  квантовой механики.

Источник

Линейчатые спектры и закономерности в них

Изучая соотношение частот разных спектральных линий в видимой области спектра атома водорода, Бальмер вывел эмпирическую формулу, которая описывала наблюдаемые частоты и позволила предсказать ряд других, ранее не наблюдавшихся. Позднее другими исследователями были получены аналогичные соотношения для частот спектральных линий, входящих в другие области спектра водорода (ультрафиолетовую и инфракрасную). С учётом всех этих данных обобщённая формула Бальмера имеет вид:

(4)

где — частота, испускаемого света; i = 1, 2, 3, 4 — целое число, характеризующее серию линий; n = i +1, i + 2, . — целое число, характеризующее конкретную линию серии; R = 3,28·10 15 с –1 — постоянная Ридберга. При i = 1 описывается так называемая серия Лаймана в ультрафиолетовой области, при i = 2 — серия Бальмера в видимой области, при n = 3, 4, 5 — серии Пашена, Брэкета и Пфунда в инфракрасной области.

Простота формулы Бальмера и точность описания спектра предполагала, что эта формула не формальна, а имеет глубокий смысл, т.е. её можно получить теоретически. Бор рассмотрел атом водорода с учётом предложенных постулатов.

Боровская теория атома водорода

Электрон, двигаясь по круговой орбите радиусом r, обладает центростремительным ускорением a =  2 / r. Между электроном и ядром действует кулоновская сила притяжения F = e 2 /(4_r 2 ). По второму закону Ньютона запишется:

(5)

Здесь m и  — масса и скорость электрона; e — заряд электрона и ядра по абсолютной величине; ₀ — электрическая постоянная. Из второго постулата Бора  = nh/(2mr). Подставляя это значение в выражение (4), находим, что

(6)

Отсюда следует, что электрон движется лишь по орбитам вполне определённого, а не любого радиуса. При n = 1 получаем радиус первой боровской орбиты

r₁ = _h 2 /(me 2 ). (7)

Тогда радиусы остальных орбит определяются из соотношения

r = r₁n 2 . (8)

Формула (7) позволила оценить размеры атома водорода (~10 –10 м), который определяется радиусом вращения электрона.

Полная энергия W атома при движении электрона по орбите радиуса r складывается из кинетической энергии W_k электрона относительно ядра и потенциальной энергии W_p взаимодействия электрона с ядром, т.е. W = W_k + W_p. Уравнение (5) преобразуем к виду:

илиW_k =  (1/2)W_p, (9)

поскольку W_p =  потенциальная энергия взаимодействия двух зарядов и m 2 /2 = W_k  кинетическая энергия электрона. Учитывая это и выражение (9), получаем, что W= (1/2)W_p = . Подставляя в эту формулу соотношение (6), находим:

(10)

где n может принимать только целые значения 1, 2, 3, . . Величину n в квантовой физике называют главным квантовым числом.

На основе выше сказанного можно объяснить природу линейчатых спектров. Согласно третьему постулату Бора, энергия испущенного или поглощённого кванта с учётом (10) равна:

h = W_n  W_i = (11)

(12)

Сравнивая это выражение с соотношением (4), видим, что теоретическим путём была получена формула Бальмера. Постоянная Ридберга вычисленная по формуле и найденная экспериментально совпадают.

Таким образом, теория Бора позволила вычислить энергию атома водорода, его размеры и объяснить происхождение линейчатых спектров. Слабой стороной теории Бора была внутренняя логическая противоречивость: с одной стороны, она использовала классическую теорию (закон Ньютона), с другой  новые квантовые представления (постулаты Бора). После открытия волновых свойств вещества стало совершенно ясно, что теория Бора явилась только переходным этапом на пути создания новой последовательной теории атомных явлений  квантовой механики.

Источник