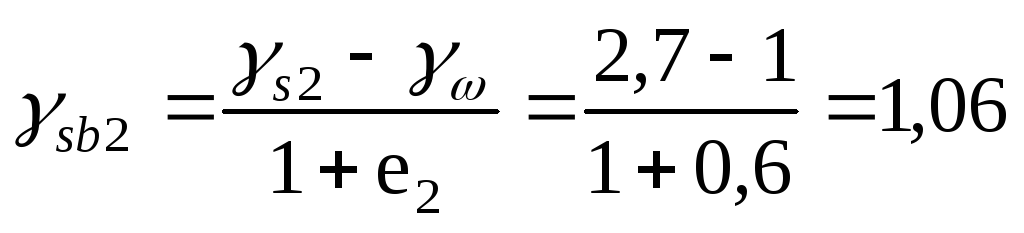3. Определение напряжений в массиве грунта от действия собственного веса (бытовое давление)
На практике используют упрощенную методику расчета, основанную на предположении о том, что природные напряжения в массиве грунта формируются только под действием собственного веса [3 8]. Также принято считать, что все деформации массива от собственного веса прекратились и напряжения полностью стабилизировались. Практический интерес представляют значения сжимающих напряжений σz.
При горизонтальной поверхности массива грунта однородного напластования сжимающие напряжения на глубине z определяются выражением
,
где γ – удельный вес грунта.
Эпюра природных напряжений массива грунта однородного напластования при горизонтальной поверхности будет иметь вид треугольника (рис. 6 а).
При неоднородном напластовании или наличии подземных вод, а также при горизонтальной поверхности напряжения от собственного веса грунтов будут определяться отдельно для каждого слоя (рис. 6 б). Причем удельный вес грунта, расположенного ниже уровня подземных вод, будет определяться с учетом взвешивающего действия воды γsb:
,
где γs – удельный вес частиц грунта; γω – удельный вес воды, принимается равным 1 т/м 3 ; е – коэффициент пористости грунта.
Рис. 6. Эпюры распределения напряжений от собственного веса грунтов
Если ниже уровня подземных вод залегает водоупорный слой, то на его кровле дополнительно учитывают давление от столба вышерасположенной воды равное γω·hω (рис. 6 в).
Пример 6. Определить напряжения от собственного веса грунтов и построить эпюру распределения данных напряжений по скважине № 1. Исходные данные см. примеры 1 и 2.
Первоначально на основании данных инженерно-геологических изысканий (см. пример 2) строим в масштабе геологическую колонку с указанием мощности слоев грунта, уровней подземных вод и водоупора (рис. 7). Далее на основании результатов определения физико-механических характеристик грунтов (см. пример 1) для каждого слоя грунта указываем необходимые для дальнейшего расчета данные.
Рис. 7. Совмещенная схема геологической колонки и эпюры
распределения напряжений от собственного веса грунтов
Расчет напряжений от собственного веса грунтов проводим последовательно, начиная от поверхности земли. Расчетные точки располагаем на поверхности земли, на границах слоев грунтов, на уровнях подземных вод и водоупора.
На поверхности земли дополнительная пригрузка отсутствует, поэтому напряжение равно .
Напряжение на границе между первым и вторым слоями грунта определяем как сумму напряжений σ1 и от собственного веса грунта первого слоя:
т/м 3 .
Напряжение на уровне подземных вод определяем как сумму напряжений σ2 и от собственного веса грунта второго слоя на расстоянии от его кровли до уровня подземных вод:
т/м 3 .
Напряжение на границе между вторым и третьим слоями грунта определяем как сумму напряжений σ3 и от собственного веса грунта второго слоя на расстоянии от уровня подземных вод до его подошвы, при этом учитываем взвешивающее действие воды на частицы грунта второго слоя
т/м 3 ,
где т/м 3 .
Напряжение на границе между третьим и четвертым слоями грунта определяем как сумму напряжений σ4 и от собственного веса грунта третьего слоя, при этом учитываем взвешивающее действие воды на частицы грунта третьего слоя
т/м 3 ,
где т/м 3 .
На кровле четвертого слоя напряжение определяем с учетом дополнительного напряжения от столба вышерасположенной воды как сумму напряжений σ5 и от собственного веса столба вышерасположенной воды:
т/м 3 .
На уровне нижней границы скважины напряжение определяем как сумму напряжений σ6 и от собственного веса грунта четвертого слоя на расстоянии от его кровли до уровня забоя скважины:
т/м 3 .
Далее по полученным значениям σ1–σ7 в масштабе строим эпюру распределения напряжений от собственного веса грунтов, которую совмещаем с уже построенной геологической колонкой (рис. 7).
Источник
Природное вертикальное напряжение в грунтах и учёт его при определении осадки фундамента. Возможные виды эпюр природного напряжения.
Природное напряжённое состояние грунтов обычно выражают эпюрой вертикальных природных напряжений, которая, согласно формуле , для однородного массива имеет вид треугольника.
Основания фундаментов, особенно гидротехнических сооружений, имеющих, как правило, широкую подошву, зачастую бывают сложены неоднородными грунтами, а вернее, состоят из нескольких слоёв грунта, различным по составу и свойствам.
В этом случае напряжение в нижележащих слоях определяют суммированием напряжений от каждого вышележащего слоя, а каждый отдельный, сложенный одним грунтом слой считают однородным и напряжение от собственного веса грунта каждого слоя определяют по формуле или . Но кроме наличия в том или ином слое грунтовой свободногравитационной воды, учитывают наличие водонепроницаемого слоя и слоя с напорными грунтовыми водами, а для построения эпюры природных вертикальных напряжений на заданной вертикальной оси геологического разреза выделяют характерные точки. Тогда с учётом вышескозанного в каждой i-ой характерной точке природное вертикальное напряжение можно найти по формуле: , где — природное напряжение в предыдущей характерной точке, — удельный вес слоя грунта, в котором находится характерная точка,
— мощность этого слоя (до i-ой характерной точки).
При расчёте оснований следует учитывать прогнозируемое изменение природных условий существования грунтов, например изменение уровня грунтовых вод. При подъёме уровня грунтовых вод в результате взвешивающего действия воды природное напряжение уменьшается и может произойти разуплотнение грунта, а при понижении, наоборот – уплотнение.
35. Сопротивление грунтов сдвигу. Сущность, нормативные и расчетные прочностные характеристики, практическое приложение закономерностей сопротивления грунтов сдвига.
Изучение сопротивления грунтов сдвигающим усилиям, возникающим в результате воздействия различных инженерных сооружений, имеет большое значение для правильного расчета устойчивости оснований (несущей способности оснований), оценки устойчивости откосов, расчета давления грунтов на подпорные стенки и других инженерных расчетов.
В настоящее время нет единой точки зрения на природу сопротивления глинистых пород сдвигу. Одни исследователи считают, что сопротивление глинистых пород сдвигу обусловлено только сцеплением между частицами, показателем которого является коэффициент сцепления. Другие полагают, что сопротивление глинистых пород сдвигу зависит как от сил трения, так и от сил сцепления. Показателями сил трения, действующих в грунте, считают угол внутреннего трения и коэффициент трения.
Вследствие неясности природы сопротивления глинистых пород сдвигу и условности разделения его на внутреннее трение и сцепление, некоторые исследователи предлагают вообще отказаться от такого разделения и характеризовать сопротивление глинистых пород сдвигу так называемым углом сдвига φ соответственно тангенс этого угла называют коэффициентом сдвига tgφ.
Сопротивление сдвигу одного и того же грунта непостоянно и зависит от физического состояния грунта — степени нарушенности естественной структуры, плотности, влажности, а также от условий производства испытаний (конструкция прибора, размеры образца, скорость сдвига и т. д.). Для получения наиболее достоверных данных испытания на сдвиг должны всегда проводиться в условиях, максимально приближающихся к условиям работы грунта под сооружением или в самом сооружении.
Показатели сопротивления грунта сдвигу определяются различными способами, среди которых можно выделить три группы:
· • способы определения сопротивления сдвигу по одной или двум заранее фиксированным плоскостям в сдвиговых приборах;
· • способы определения сопротивления сдвигу путем раздавливания при одноосном и трехосном сжатии;
· • способ определения сопротивления сдвигу по углу естественного откоса.
Способы первой группы могут быть в свою очередь разделены на две подгруппы:
· а) способы поперечного сдвига с конечной плоскостью сдвига;
· б) способы кольцевого сдвига с бесконечной (замкнутой) плоскостью сдвига.
Лабораторные испытания грунтов для определения показателей трения и сцепления способом поперечного сдвига производят путем среза нескольких образцов исследуемого грунта. При этом в зависимости от характера предварительной подготовки образцов к опыту различают:
· а) сдвиг нормально уплотненных образцов (завершенное уплотнение), когда образцы перед опытом предварительно уплотняются под разными нагрузками до окончания процесса консолидации; срез каждого образца производится при той же вертикальной нагрузке, под которой он предварительно уплотнялся;
· б) сдвиг переуплотненных образцов, когда образцы предварительно уплотняются до окончания процесса консолидации, а сдвигаются без нагрузки или при меньших нагрузках;
· в) сдвиг недоуплотненных образцов (незавершенное уплотнение), когда образцы предварительно не уплотняются или уплотняются в продолжение короткого времени, за которое не наступает полная консолидация; срез производится при различных вертикальных нагрузках.
В зависимости от скорости приложения сдвигающего усилия в процессе опыта различают медленный сдвиг и быстрый сдвиг. При медленном сдвиге сдвигающую силу увеличивают только после прекращения деформации, вызванной предыдущей ступенью этой силы. При быстром сдвиге увеличение сдвигающей силы производят быстро, не дожидаясь прекращения деформаций.
Источник