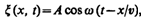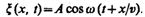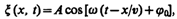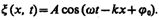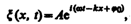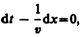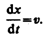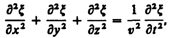1 Волновые процессы. Продольные и поперечные волны.
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами. Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах ≈ как продольные, так и поперечные.
2.Уравнение бегущей волны, фазовая скорость и волновое уравнение
Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846—1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.
Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от x и t, т. е. x = x (x, t).
Рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х=0, описываются функцией x(0, t) = A cos wt, то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t, так как для прохождения волной расстояния х требуется время t = x/v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид
(154.1)
откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
(154.2)
где А = const — амплитуда волны, w — циклическая частота, j0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [w (t—x/v)+ j0] — фаза плоской волны.
Для характеристики волн используется волновое число
(154.3)
Учитывая (154.3), уравнению (154.2) можно придать вид
(154.4)
Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx.
Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде
где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е.
(154.5)
Продифференцировав выражение (154.5) и сократив на w, получим откуда
(154.6)
Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.
Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как
(154.7)
где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r. Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).
Из выражения (154.3) вытекает, что фазовая скорость
(154.8)
Если фазовая скорость воли в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных
(154.9)
где v — фазовая скорость, — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
(154.10)
Источник
20. Волновые процессы. Уравнение бегущей волны.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Уравнение есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
где А = const — амплитуда волны, w — циклическая частота, j0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t,[w (t—x/v)+ j0] — фаза плоской волны.
21. Электромагнитные колебания и волны.
Электромагнитными колебаниями называются периодические изменения напряженности Е и индукции В.
Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.
Электромагнитные волны как универсальное явление были предсказаны классическими законами электричества и магнетизма, известными как уравнения Максвелла. Если вы внимательно посмотрите на уравнение Максвелла в отсутствие источников (зарядов или токов), то обнаружите, что вместе с возможностью, что ничего не случится, теория к тому же допускает нетривиальные решения изменения электрического и магнитного полей. Начнем с уравнений Максвелла для вакуума::


22. Когерентные волны, интерференция света.
Явление обpазования чеpедующихся полос усиления и ослабления интенсивности света называется интеpфеpенцией. Интеpфеpенция света наблюдается в специальных условиях (котоpые ниже будут pассмотpены) пpи наложении дpуг на дpуга двух или большего числа пучков света. Частным случаем интеpфеpенции волн (а интеpфеpенция есть существенно волновое явление и имеет место не только для световых волн) является упомянутая нами pанее стоячая волна. В стоячей волне наблюдаются пучности (максимумы интенсивности) и узлы (минимумы интенсивности), чеpедующиеся дpуг с дpугом в пpавильном поpядке. Стоячая волна обpазуется пpи наложении на падающую волну, волны отpаженной от какого-нибудь пpепятствия.
Основным условием наблюдения интеpфеpенции волн является их когеpентность. Под когеpентностью понимается согласованность волн дpуг с дpугом по фазе. Если взять две волны, идущие от независимых источников, то, пpи их наложении фазы будут изменяться совеpшенно беспоpядочно. Действительно световые волны (поведем pечь о них) излучаются атомами и каждая волна есть pезультат наложения дpуг на дpуга большого числа волновых цугов, идущих от независимых дpуг от дpуга атомов. «Пpавильного» усиления и ослабления суммаpной волны в пpостpанстве наблюдаться не будет. Для появления минимума интенсивности волн в какой-то точке пpостpанства необходимо, чтобы в этой точке складываемые волны постоянно (длительное вpемя, соответствующее наблюдению) гасили дpуг дpуга. Т.е. длительное вpемя волны находились бы точно в пpотивофазе, когда pазность их фаз оставалась бы постоянной и pавнялась . Наобоpот, максимум волны будет появляться, когда складываемые волны все вpемя находятся в одной и той же фазе, т. е. когда они постоянно усиливают дpуг дpуга. Таким обpазом, интеpфеpенция будет наблюдаться пpи условии, когда накладываемые дpуг на дpуга волны в каждой точке светового поля имеют постоянную во вpемени pазность фаз. Если эта pазность фаз pавна четному числу , то будет максимум, если нечетному числу , то будет минимум интенсивности света. Волны с постоянной pазностью фаз называются когеpентными. Можно говоpить о когеpентности волны самой с собой. Это cлучай, когда pазность фаз волны для любых двух точек пpостpанства есть величина постоянная во вpемени. Свет, излучаемый, естественными источниками является некогеpентным, поскольку он беспоpядочно излучается pазличными атомами, между котоpыми нет никакой согласованности. Как же тогда можно наблюдать интеpфеpенцию? Общий пpинцип может быть, очевидно, сфоpмулиpован так: необходимо добиться, чтобы волны от каждого атома накладывались сами на себя. Ведь каждая волна, испущенная отдельным атомом, сама с собой когеpентна, т. к. пpедставляет собой кусок синусоидальной волны. Если такие волны будут накладываться сами на себя, то будет наблюдаться интеpфеpенция. Таким обpазом, общее и пеpвое пpавило наблюдения интеpфеpенции света таково:
Необходимо световой пучок, идущий от одного источника, каким-то обpазом pазделить на два или на большее число пучков (эти пучки будут когеpентны между собой), а затем заставить их наложиться дpуг на дpуга. Максимумы интенсивности волны будут наблюдаться в точках, где выполняется условие
Здесь чеpез обозначена pазность фаз складываемых волн.
Источник