Примеры симметрии в природе
Скорее всего, вы неоднократно проходили в магазине мимо полки с капустой брокколи Романеско и из-за её необычного вида предполагали, что это генно-модифицированный продукт. Но на самом-то деле, это всего лишь ещё один из многих примеров фрактальной симметрии в природе – хотя и безусловно поразительный.
В геометрии фрактал — это сложный узор, каждая часть которого обладает тем же геометрическим рисунком, что и весь узор в целом.
Поэтому в случае капусты брокколи Романеско каждый цветок компактного соцветия обладает той же логарифмической спиралью, что и вся головка (просто в миниатюрном виде). По сути, вся головка этой капусты — это одна большая спираль, которая состоит из маленьких почек похожих на шишки, которые также растут в виде мини-спиралей. Кстати говоря, капуста брокколи Романеско является родственницей, как капусты брокколи, так и цветной капусты, хотя её вкус и консистенция больше напоминают цветную капусту.
Она также богата каротиноидами и витаминами С и К, что означает, что она является полезным и математически красивым дополнением к нашей пище.
Медовые соты
Пчёлы это не только ведущие производители мёда – они также знают толк в геометрии.
Тысячи лет люди поражались совершенству гексагональных форм в медовых сотах и задавались вопросом о том, как же пчёлы могут инстинктивно создавать такие формы, которые человек может создавать только с линейкой и компасом.
Медовые соты являются предметов обойной симметрии, где повторяющийся узор покрывает плоскость (например, плиточный пол или мозаика). Так каким же образом и почему пчёлы так любят строить шестиугольники?
Начнём с того, что математики считают, что эта совершенная форма позволяет пчёлам запасать самое большое количество мёда, используя наименьшее количество воска. При строительстве других форм у пчёл получались бы большие пространства, так как такие фигуры, как например круг – не прилегают друг к другу полностью.
Другие наблюдатели, которые менее склонны верить в сообразительность пчёл, считают, что они формируют гексагональную форму совершенно «случайно». Другими словами, пчёлы на самом деле делают круги, а воск сам по себе принимает гексагональную форму.
В любом случае – это произведение природы и довольно-таки потрясающее.
Подсолнухи
Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии чисел, известным как последовательность Фибоначчи. Последовательность Фибоначчи это: 1, 2, 3, 5, 8, 13, 21, 24, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел). Если не жалея времени заняться подсчётом количества семенных спиралей в подсолнечнике, мы бы обнаружили, что количество спиралей совпадает с числами Фибоначчи.
Более того, огромное количество растений (включая капусту брокколи Романеско) отпускают лепестки, листья и семена в соответствии с последовательностью Фибоначчи, именно поэтому так сложно найти четырёхлистный клевер.
Считать спирали на подсолнечнике может быть довольно трудно, поэтому, если вы хотите самостоятельно проверить этот принцип, попробуйте подсчитать спирали на более крупных вещах, таких как шишки, ананасы, и артишоки.
Но почему цветы подсолнечника и другие растения подчиняются математическим правилам? Как и в случае шестиугольников в улье, всё дело в эффективности. Чтобы не углубляться в технические особенности, можно просто сказать, что цветок подсолнечника может вместить наибольшее количество семян, если каждое семечко расположено под углом, представляющим собой иррациональное число.
Оказывается, самым иррациональным числом является золотое сечение, или Фи, и так уж случилось, что, если мы разделим любое число Фибоначчи или Лукаса на предыдущее число в последовательности, мы получим число, близкое к Фи (+1,618033988749895 …). Таким образом, в любом растении, растущем в соответствии с последовательностью Фибоначчи, должен быть угол, который соответствует Фи (углу равному числу золотого сечения) между каждым из семян, листьев, лепестков, или веток.
Раковина Наутилуса
Помимо растений существуют также некоторые животные, демонстрирующие собою числа Фибоначчи. Например, раковина Наутилуса выросла в «Спираль Фибоначчи». Спираль образуется в результате попытки раковины поддерживать ту же пропорциональную форму по мере своего роста наружу. В случае наутилуса, такая тенденция роста позволяет ему сохранять одинаковую форму тела в течение всей своей жизни (в отличие от людей, чьи тела изменяют свои пропорции по мере взросления). Как и следовало бы ожидать – в этом правиле существуют и исключения: не каждая раковина наутилуса вырастает в спираль Фибоначчи.
Но все они растут в виде своеобразных логарифмических спиралей. И, до того как вы начнёте задумываться над тем, что эти головоногие, пожалуй, знают математику лучше вас, помните, что их раковины растут в такой форме неосознанно для них, и что они просто пользуются эволюционным дизайном, который позволяет моллюску расти, не изменяя форму.
Животные
Большинство животных обладает двусторонней симметрией, это означает, что их можно разделить на две одинаковые половины, если линию деления провести по их центру тела. Даже люди обладают двусторонней симметрией, и некоторые учёные считают, что симметрия человека является самым важным фактором того, будем ли мы считать его физически привлекательным или нет.
Другими словами, если у вас кривобокое лицо, надейтесь, что у вас есть целая уйма компенсирующих, положительных качеств.
Одно животное, скорее всего, воспринимает важность симметрии в брачных ритуалах слишком серьёзно, и этим животным является павлин. Дарвина очень раздражал этот вид птиц, и в своём письма в 1860 году он написал, что «каждый раз, когда я смотрю на перо из павлиньего хвоста – меня тошнит!». Для Дарвина хвост павлина казался чем-то обременительным, так как, по его мнению, такой хвост не имел эволюционного смысла, так как он не подходил под его теорию «естественного отбора».
Он злился до тех пор, пока он не разработал теорию сексуального отбора, которая заключается в том, что животное развивает у себя определённые качества, которые обеспечат ему лучший шанс спариться. Очевидно, для павлинов сексуальный отбор считается невероятно важным, так как они отрастили себе различные варианты узоров, чтобы привлечь своих дам, начиная с ярких цветов, большого размера, симметрии своих тел и повторяющемся узоре их хвостов.
Паутины пауков
Существует примерно 5 000 видов пауков-кругопрядов, и все они создают практически совершенно круглые паутины с почти равноудаленными радиальными опорами, исходящими из центра и связанными по спирали для более эффективной ловли добычи.
Ученые до сих пор не нашли ответа на вопрос, почему пауки-кругопряды делают такой большой акцент на геометрию, так как исследования показали, что округлая паутина не удерживает добычу лучше, чем паутина неправильной формы. Некоторые ученые предполагают, что пауки строят круглые паутины из-за того, что они более прочные, и радиальная симметрия помогает равномерно распределить силу удара, когда жертва попадает в сети, в результате чего в паутине оказывается меньше разрывов.
Но остается вопрос: если это действительно лучший способ создания паутины, то почему не все пауки его используют?
У некоторых пауков, не являющихся кругопрядами, есть возможность создавать такую же паутину, однако они этого не делают. Например, недавно обнаруженный в Перу паук строит отдельные части сети одинакового размера и длины (что доказывает его способность «замерять»), но затем он просто соединяет все эти части одинакового размера в случайном порядке в большую паутину, которая не обладает какой-то определённой формой. Может быть эти пауки из Перу знают что-то, чего не знают пауки-кругопряды, или же они ещё просто не оценили всю прелесть симметрии?
Круги на полях с урожаем
Дайте парочке шутников доску, кусок верёвки и покров тьмы и окажется, что люди тоже хороши в создании симметричных форм.
На самом деле, именно из-за невероятной симметрии и сложности дизайна кругов на полях с урожаем, люди продолжают верить, что только пришельцы из космоса способны сотворить такое, даже несмотря на то, что люди, создавшие эти круги, сознались. Возможно, когда-то и была смесь кругов сделанных людьми с теми, которые сделали пришельцы, но прогрессирующая сложность кругов является самым явным доказательством того, что их сделали именно люди.
Было бы нелогичным предположить, что пришельцы сделают свои послания ещё сложнее, учитывая то, что люди ещё толком не разобрались в значении простых посланий. Скорее всего, люди учатся друг у друга по примерам созданного и всё больше и больше усложняют свои творения. Если отбросить в стороны разговоры об их происхождении, можно точно сказать, что на круги приятно смотреть, по большей части из-за того, что они так геометрически впечатляющи.
Физик Ричард Тейлор (Richard Taylor) провёл исследование кругов на полях и обнаружил, что помимо того факта, что за ночь на земле создается по крайней мере один круг, большинство их дизайнов отображают широкий спектр симметрии и математических моделей, в том числе фракталов и спиралей Фибоначчи.
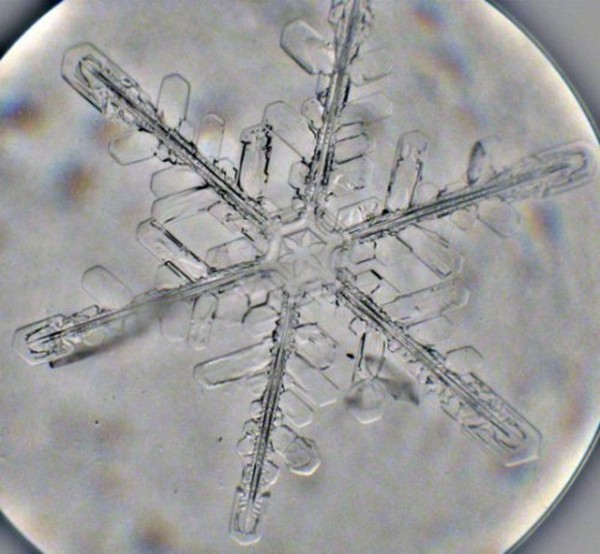
Снежинки
Даже такие крошечные вещи как снежинки тоже образуются по законам порядка, так как большинство снежинок формируются в виде шестикратной радиальной симметрии со сложными, идентичными рисунками на каждой из её ветвей.
Понять, почему растения и животные выбирают симметрию, сложно само по себе, но неодушевлённые объекты – как же им это удаётся? По-видимому, всё сводится к химии, и в частности к тому, как молекулы воды выстраиваются по мере своего замерзания (кристаллизуются).
Молекулы воды приходят в твёрдое состояние путём образования слабых водородных связей друг с другом. Эти связи выравниваются в упорядоченном расположении, которое максимизирует силы притяжения и снижает силы отталкивания, что как раз и является причиной образования гексагональной формы снежинки. Однако всем нам известно, что двух одинаковых снежинок не бывает, так как же снежинка формируется в абсолютной симметрии сама с собой, но не похожа на другие снежинки? По мере того как каждая снежинка падает с неба она проходит через уникальные атмосферные условия, такие как температура и влажность, которые влияют на то, как кристаллы «растут» на ней. Все ветви снежинки проходят через одни и те же условия и следовательно кристаллизуются одинаковым образом — каждая ветвь является точной копией другой. Ни одна другая снежинка не проходит через те же условия по мере своего спуска, поэтому они все выглядят немного по-разному.
Галактика Млечный Путь
Как мы уже видели, симметрия и математические узоры существуют повсюду, куда бы мы ни посмотрели – но ограничены ли эти законы природы только нашей планетой? По всей видимости – нет.
Недавно обнаружив новую часть Млечного Пути, астрономы считают, что наша галактика является почти совершенным отражением самой себя. Основываясь на новой информации, учёные получили подтверждение своей теории о том, что в нашей галактике есть только два огромных рукава: Персей и Рукав Центавра. В дополнение к зеркальной симметрии, Млечный Путь обладает ещё одним удивительным дизайном – похожим на раковины наутилуса и подсолнуха, где каждый рукав галактики представляет собой логарифмическую спираль, берущую начало в центре галактики и расширяющуюся к внешнему краю.
Симметрия Солнца и Луны
Учитывая, что диаметр солнца составляет 1,4 миллиона километров, а диаметр луны всего 3,474 километра, очень сложно представить себе, что Луна может закрывать собой солнечный свет и давать нам около пяти солнечных затмений каждые два года.
Так как же это всё-таки происходит?
По совпадению, несмотря на то, что ширина солнца примерно в четыреста раз больше ширины луны, оно расположено от нас в четыреста раз дальше, чем луна. Симметрия этого соотношения приводит к тому, что нам кажется, что солнце и луна, одинаковые по размеру, если смотреть с Земли, поэтому луна может с лёгкостью блокировать солнце, когда они находятся на одной линии по отношению к Земле.
Расстояние от Земли до солнца, конечно, может вырасти во время её выхода на орбиту, и когда в это время случается затмение, мы можем полюбоваться ежегодным или неполным затмением, так как солнце не полностью закрыто. Но каждый год или два, всё становится абсолютно симметричным, и мы можем посмотреть на великолепное событие, которое мы называем полным солнечным затмением.
Источник