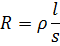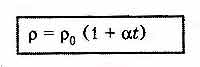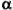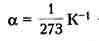Электрический ток в металлах: подробное объяснение
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток — это упорядоченный поток носителей электрического заряда. Носители — это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
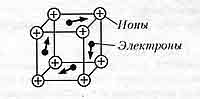
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в «облако» хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как «ро»). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление — это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10 -8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10 -8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10 -8 |
| Медь | 1.72*10 -8 |
| Алюминий | 2.82*10 -8 |
| Вольфрам | 5.6*10 -8 |
| Железо | 10*10 -8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью «свободным», поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E — сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя — он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ — средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10 -4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 10 6 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика — несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Источник
Природа электрического тока в металлах. Сверхпроводимость
Металлы – хорошие проводники электрического тока. Проводимость в металлах обусловлена наличием в них свободных электронов, которые сравнительно легко отрываются от атомов. Образуя положительный ион и свободный электрон.
В отсутствие электрического поля электроны движутся беспорядочно, участвуя в тепловом (хаотическом) движении.
Под действием электрического поля электроны начинают упорядоченно перемещаться между ионами, находящимися в узлах кристаллической решетки, со средней скоростью порядка 10 -4 м/с, образуя электрический ток.
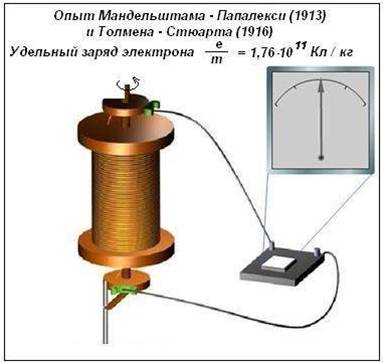
Экспериментальное доказательство того, что проводимость металлов обусловлена движением свободных электронов, было дано в опытах Л.И. Мандельштама и Н.Д. Папалекси в 1912г (результаты не были опубликованы), а также Т. Стюарта и Р. Толмена в 1916 г.
Идея опытов: если резко тормозить движущийся кусок металла, то находящиеся в нем свободные заряды, двигаясь по инерции, будут скапливаться у переднего его конца, и между концами проводника возникает разность потенциалов.
Опыт Мандельштама и Папалекси
Катушка, соединенная с телефоном, приводилась в колебательное движение вокруг своей оси. Благодаря инерции свободный зарядов на концах катушки возникала переменная разность потенциалов, и телефон издавал звук.
Это были лишь качественные опыты. Никакие измерения и количественные расчеты в этих опытах не были произведены.
Катушка большого диаметра с намотанным на ней металлическим проводом приводилась в быстрое вращение и затем резко тормозилась. При торможении катушки свободные заряды в проводнике продолжали некоторое время двигаться по инерции. Вследствие движения зарядов относительно проводника в катушке возникал кратковременный электрический ток, который регистрировался гальванометром присоединённым к концам проводника с помощью скользящих контактов.
Направление тока свидетельствовало о том, что он обусловлен движением отрицательно заряженных частиц.
Измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение q0/m. Оно оказалось равным 1,8*1011Кл/кг. Это значение совпадает со значением аналогичного отношения для электрона, найденным из других опытов.
Таким образом было экспериментально установлено, что носителями электрического тока в металлах являются свободные электроны.
Зависимость сопротивления проводника R от температуры:
При нагревании размеры проводника меняются мало, а в основном меняется удельное сопротивление.
Удельное сопротивление проводника зависит от температуры:
где ро — удельное сопротивление при 0 градусов, t — температура, — температурный коэффициент сопротивления (т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)
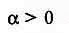
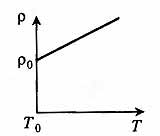
Для металлов и сплавов
Обычно для чистых металлов принимается
Таким образом, для металлических проводников с ростом температуры
увеличивается удельное сопротивление, увеличивается сопротивление проводника и уменьшается эл.ток в цепи.
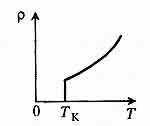
Низкотемпературная сверхпроводимость:
наблюдается при сверхнизких температурах (ниже 25 К) во многих металлах и сплавах; при таких температурах удельное сопротивление этих веществ становится ничтожно малым.
В 1986 г. открыта (для металлокерамики) высокотемпературная сверхпроводимость (при 100 К).
Трудность достижения сверхпроводимости:
— необходимость сильного охлаждения вещества
Область применения:
— получение сильных магнитных полей;
— мощные электромагниты со сверхпроводящей обмоткой в ускорителях и генераторах.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник