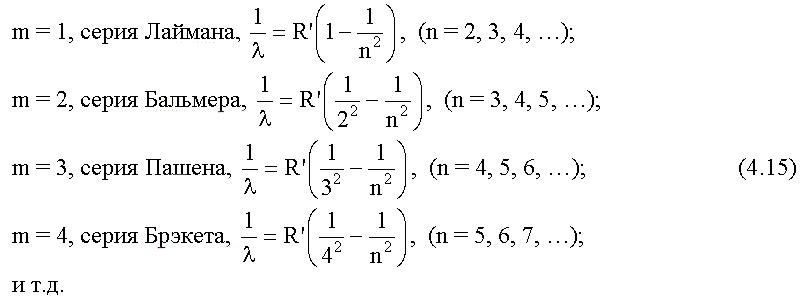Природа излучения атома водорода

Атом водорода. Линейчатые спектры

Самым простым из всех атомов является атом водорода, и он выступил в свое время в качестве своеобразного тест-объекта для теории Бора. К моменту появления теории атом водорода был тщательно исследован в ходе экспериментов: имелось знание о том, что он содержит единственный электрон. Ядром атома является протон.

Квантовое число m введено в связи с тем, что проекция момента импульса на любое выделенное в пространстве направление (к примеру, направление вектора B → магнитного поля) также принимает дискретный ряд значений.

Все виды квантовых чисел ( n , l , m ) находятся во взаимосвязи с правилами квантования. К примеру, орбитальное квантовое число l может принимать значения целого числа от 0 до ( n – 1 ) . Магнитное квантовое число m может принимать любые значения целого числа в интервале ± l . Тогда каждому значению главного квантового числа n , описывающему состояние энергии атома, соответствует целый ряд комбинаций квантовых чисел l и m . Одновременно с этим, с каждой такой комбинацией соотносится определенное распределение вероятности | Ψ | 2 обнаружения электрона в разных точках пространства («электронное облако»).

s -состояния ( 1 s , 2 s , . . . , n s , . . . ) – это состояния, при которых орбитальное квантовое число l равно нулю.

Описываются s -состояния сферически симметричными распределениями вероятности.

Когда l > 0 сферическая симметрия электронного облака нарушается.

p -состояния — это состояния при l = 1 .

d -состояния – это состояния при l = 2 и т.д.

Рис. 6 . 3 . 4 иллюстрирует кривые распределения вероятности ρ ( r ) = 4 π r 2 | Ψ | 2 обнаружения электрона в атоме водорода на разных расстояниях от ядра в состояниях 1 s и 2 s .

Рисунок 6 . 3 . 4 . Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1 s и 2 s . r 1 = 5 , 29 · 10 – 11 м – радиус первой орбиты Бора.

На рисунке 6 . 3 . 4 наглядно продемонстрировано, что электрон в состоянии 1 s (основное состояние атома водорода) имеет возможность быть обнаруженным на различных расстояниях от ядра. С самой высокой вероятностью электрон обнаружится на расстоянии, равном радиусу r 1 первой боровской орбиты. Вероятность нахождения электрона в состоянии 2 s достигает максимума на расстоянии r = 4 r 1 от ядра. И в том, и в том случае атом водорода возможно представить, как сферически симметричное электронное облако, в центре которого расположено ядро.

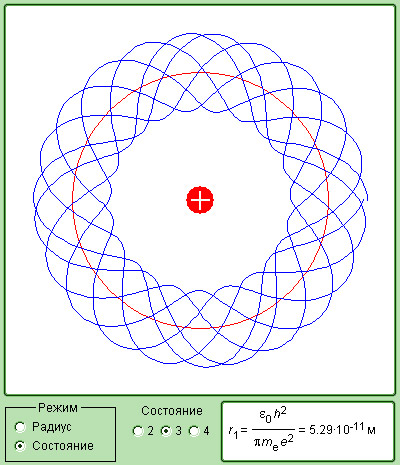
Рисунок 6 . 3 . 5 . Модель квантования электронных орбит.

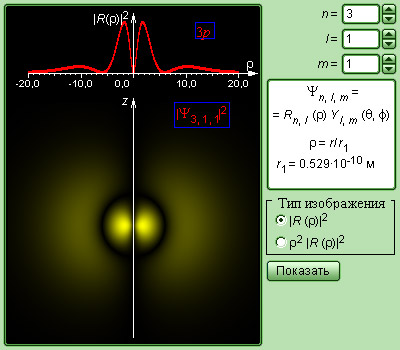
Рисунок 6 . 3 . 6 . Модель атома водорода.

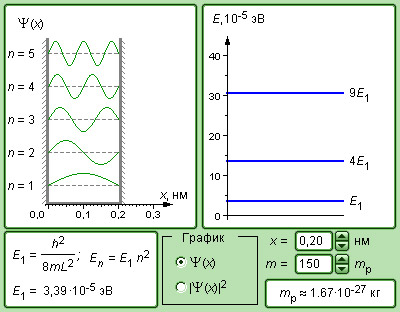
Рисунок 6 . 3 . 7 . Модель частицы в потенциальной яме.

Источник

§ 2. Спектры излучения атома водорода в теории Бора

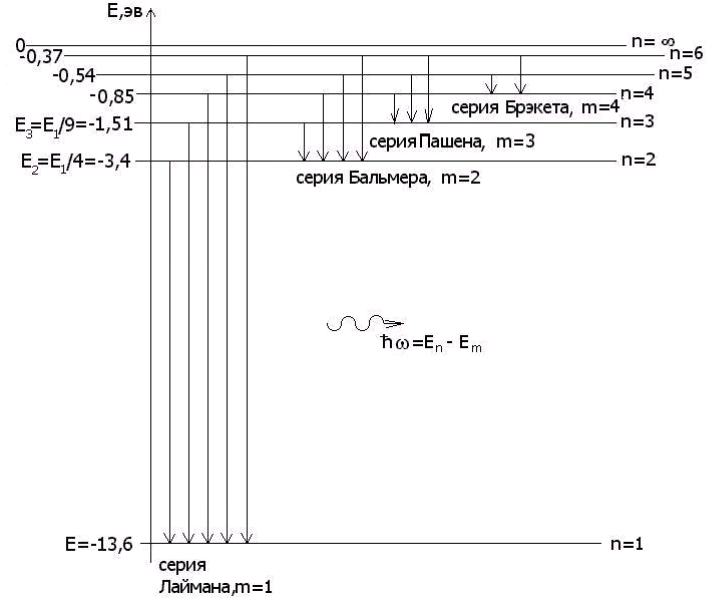
Изобразим на рис. 4.2. в масштабе энергетические уровни атома водорода E_n в зависимости от главного квантового числа n, в соответствии с формулой (4.10).

Согласно второму постулату Бора (4.4.) энергия излученного фотона, , равна разности энергий стационарных состояний, между которыми происходит квантовый переход:

, в случае излучения n > m.

Подставляя сюда выражения для E_n и E_m, (4.8) для частоты n, получим:

— постоянная Ридберга, она так названа в честь шведского физика И. Ридберга.

Так как λ = c/v, то для длины волны λ получим следующее выражение:

— тоже называют постоянной Ридберга.

Из теории Бора следует, что спектр атома водорода имеет линейчатый характер, причем, наблюдаемые линии объединены в спектральные серии. Задается серия номером m уровня, на который происходит квантовый переход. Первые серии названы именами ученых-физиков:

Спектры атома водорода были изучены экспериментально до создания Бором своей теории. Хорошее совпадение экспериментальных данных с выводами теории Бора для спектров атома водорода говорит в пользу этой теории.

Однако, попытки применить теорию Бора к более сложным атомам потерпели неудачу. В настоящее время теория атома Бора представляет исторический интерес как промежуточный этап к созданию более верной теории. Такая теория теперь существует — это квантовая механика.

Итоги лекции n 4

1. Уравнение движения электрона в планетарной модели атома, записанное на основе второго закона Ньютона, позволяет атому иметь любой размер, опыт же показывает, что размеры атомов порядка 10 -10 м. Это противоречие теории и опыта получило название проблемы размера атома.
2. Проблема стабильности атомасостояла в том, что в планетарной модели атома электрон, двигаясь по окружности, должен, из-за наличия ускорения, непрерывно излучать энергию и через время ~10 -8 с упасть на ядро. Однако, весь наш опыт весомо свидетельствует о стабильности атомов.
3. Проблемы эти были решены в 1913 г. Н. Бором на основе его двух постулатов:

1) существуют стационарные состояния атом, находясь в которых он не излучает электромагнитных волн. Условие стационарности состояния атома — квантование момента импульса электрона L: 2) излучение испускается или поглощается в виде квантов энергии при переходе электрона из одного стационарного состояния в другое. Энергия кванта равна разности энергий стационарных состояний атома, между которыми происходит переход: здесь Е_n — энергия стационарного состояния до перехода, Е_m — энергия стационарного состояния после перехода.

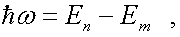
1. Дополнив механику Ньютона этими постулатами, Н. Бор получил выражения для радиусов стационарных орбит r_n (см. (4.5)):

и энергии стационарных состояний атома водорода Е_n (см. (4.8)): В этих формулах n — целое положительное число: n = 1, 2, 3.

1. Из второго постулата Бора и формулы для Е_n следует выражение, определяющее длины волн, излучаемых (и поглощаемых) атомом водорода (см. (4.12), (4.13)):

R’ называют постоянной Ридберга, ее экспериментальное значение Величину R также называют постоянной Ридбера, теория Бора дает для нее следующее выражение: Теоретическое значение R близко к ее экспериментальному значению. R = 3,29 · 10 15 1/c.

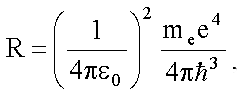
Источник

§ 209. Линейчатый спектр атома водорода

Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ вполне определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.

Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:

где R‘=1,10•10 7 м -1 — постоянная Ридберга. Так как v = c/, то формула

(209.1) может быть переписана для частот:

где R=R’с=3,29•10 15 с -1 также постоянная Ридберга.

Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями n, образуют группу или серию линий, называемую серией Бальмера. С увеличением n линии серии сближаются; значение n= определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.

В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:

В инфракрасной области спектра были также обнаружены: серия Пашена

Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:

где m имеет в каждой данной серии постоянное значение, m= 1, 2, 3, 4, 5, 6 (определяет серию), n принимает целочисленные значения начиная с m+1 (определяет отдельные линии этой серии).

Исследование более сложных спектров — спектров паров щелочных металлов (например, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.

Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.

§210. Постулаты Бора

Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885—1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу своей теории Бор положил два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

m_evr_n = nh (n=1, 2, 3, . ), (210.1)

где m_e — масса электрона, v — его скорость по n-й орбите радиуса r_n, h=h/(2). Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией

h=E_n-E_m, (210.2)

равной разности энергий соответствующих стационарных состояний (E_n и E_m — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При E_mE_n происходит излучение фотона (переход атома из состояния с большей энергией в состояние с меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при E_m>E_n — его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот v = = (E_n-E_m)/h квантовых переходов и определяет линейчатый спектр атома.

Источник