3.5. Магнитостатика
Помимо кулоновского взаимодействия зарядов, в природе существует взаимодействие посредством магнитного поля. Магнитное взаимодействие наблюдается как между макроскопическими телами, так и между отдельными частицами, в том числе и элементарными. Взаимодействовать через магнитное поле могут как заряженные, так и незаряженные тела, что указывает на отсутствие непосредственной связи магнитного взаимодействия с электростатическим. Существует большое число явлений, на первый взгляд не связанных друг с другом, которые, однако, имеют в своей основе магнитные взаимодействия. В опытах Ампера и других, относящихся к первой половине XIX века, было установлено, что между проводниками при протекании в них электрического тока возникают силы притяжения и отталкивания магнитного характера. Был установлен опытный факт возникновения магнитного поля в пространстве, окружающем проводник с током. Вместе с тем, существует ряд хороших проводников металлов, таких как железо, которые создают магнитное поле вокруг себя даже при отсутствии протекания через них электрического тока. Другими словами, эти металлы обладают собственным магнитным полем. Такие вещества называются магнетиками. Существуют магнетики и среди диэлектриков. Таким образом, весьма различные по своей природе вещества — немагнитные проводники, магнитные металлы и диэлектрики — обладают способностью создавать магнитное поле. Возникает вопрос: что может служить источником магнитного поля в указанных средах, или каков механизм его возникновения? Проще всего было бы предположить, что существуют «магнитные заряды», аналогичные электрическим. Такие предположения делались, но все попытки экспериментально обнаружить такие заряды оказались безуспешными. Следовательно, нужно считать, 3
что в природе магнитных зарядов не существует. Вместе с тем из факта возникновения магнитного поля при протекании тока по проводнику можно сделать вывод, что элементарным носителем магнитных свойств является сам элемент тока. Для обычных проводников этот вывод правдоподобен; но как быть с остальными средами? После того как было изучено строение атомов и молекул, стало ясно, что в отдельных атомах и молекулах вещества также существуют элементарные токи, связанные с движением зарядов внутри этих частиц. Эти элементарные токи также должны вносить вклад в магнитные свойства вещества. Дальнейшее изучение свойств элементарных частиц — электрона, протона и других — показало, что этим частицам присущ новый тип движения, который до тех пор не проявлялся на макроскопическом уровне. С возможностью движения такого рода также следует связать появление магнитных свойств отдельных частиц. С точки зрения механики с каждым из возможных типов движения связан вполне определенный момент импульса, то есть механический момент. Для частиц, обладающих зарядом, соответствующая этому механическому моменту магнитная величина называется магнитным моментом. Оказывается, что магнитный момент как раз и играет роль элементарного носителя магнитных свойств, являясь своего рода «элементарным магнитом». В каждой из указанных выше сред магнитные моменты имеют разную природу и величину, будучи связанными с различными типами движения зарядов. Но суммарные магнитные моменты, отвечающие всем возможным типам движения зарядов в среде, определяют величину и распределение магнитного поля в пространстве. Таким образом, происхождение магнитного поля связано с движением электрических зарядов. Тот факт, что покоящийся заряд создает электрическое поле, а движущийся — магнитное, позволяет утверждать, что электрическое и магнитное поля представляют собой вовсе не различные физические поля, а оказываются различными проявлениями одного и того же электромагнитного поля заряда. В зависимости от относительной скорости движения двух зарядов сила, действующая на заряды, будет иметь
электрический либо магнитный характер. Таким образом, представление об электрическом либо магнитном поле является относительным. В различных инерциальных системах отсчета электромагнитное поле заряда будет выглядеть по-разному. В движущейся системе отсчета, в которой заряд покоится, мы будем наблюдать только электрическое поле, а в системе координат, в которой заряд движется, — и электрическое, и магнитное поля одновременно. В частности, можно выбрать такую систему отсчета, в которой электрическое поле будет равно нулю, а магнитное — отлично от нуля. Мы будем изучать магнитное поле движущихся зарядов в покоящейся лабораторной системе отсчета. При движении заряженных частиц —электронов — в проводнике их заряд компенсирован положительным зарядом решетки. Поэтому электрическое поле вне проводника отсутствует, а возникает только магнитное поле.
3.5.2. Свойства магнитного поля. Закон Био-Савара
Как всякое другое силовое поле, магнитное поле можно характеризовать силовыми линиями. По аналогии с электрическим полем векторы, касательные к силовым линиям, являются векторами напряженности магнитного поля H . Однако в отличие от электрического поля вектор H должен быть пропорционален не величине заряда, а потоку заряда в проводнике. Найдем связь между ними. Возьмем проводник произвольной формы и мысленно разобьем его на бесконечно малые элементы (рис.). Введем вектор dl = ndl , где n – единичный вектор в направлении потока электронов в выбранном элементе. Поток заряда dI Q равен величине за- ряда в объеме проводника dQ = q n dV , ( n – плотность электронов), умноженной на скорость переноса электронов в направлении d ,
| (3.82) | |
| dI Q = qnvdV = qnvSd = qnvSd | |
Здесь мы воспользовались тем, что направления скорости и перемещения электронов в проводнике совпадают, т.е. vd = vd . Но согласно (3.58) q n v S = I , где I — сила тока, и, таким образом, поток заряда
| dI Q = Idl . | (3.83) |
Эту величину будем считать элементарным источником магнитного поля dH . Пусть мы хотим определить величину напря- женности в точке А. В силу принципа суперпозиции вектор H является векторной суммой всех бесконечно малых напряженностей dH , создаваемых всеми элементами d проводника. Поэтому, для того чтобы найти напряженность поля, создаваемую в данной точке всем проводником, нужно сначала определить величину dH , а затем просуммировать ее по всей длине проводника. Для каждого конкретного проводника вполне определенной формы ве- личина H , конечно, будет разной, но величина dH должна быть, очевидно, одинаковой. Найдем величину dH . Величина dH должна зависеть от направления, в котором точ-
| ка А видна из элемента d , то есть от угла между вектором n и | |||
| e | = | r | – единичным вектором в направлении точки А. Поскольку |
| r | r | ||
напряженность поля векторная величина, то dH должна быть пропорциональна векторному произведению векторов n и e r . dH n × e r Последнее соображение, которое нужно учесть, состоит в том, что из-за связи между электрическим и магнитным полями последнее должно убывать с расстоянием точно так же, как кулонов- ское поле, т. е. обратно пропорционально квадрату расстояния: H ~ 1/ r 2 . Суммируя все сказанное, мы приходим к необходимости записать выражение для напряженности поля элемента проводника в виде:
| dI | × e | 1 | 1 | |||
| dH = | Q | r | = | I ( d × e r ) = | I ( d × r ) (3.84) | |
| 4 π r | 2 | 4 π r | 2 | 4 π r | 3 | |
Как и в законе Кулона, в формулу для удобства добавлен множитель 1/4 π . Выражение (3.84) носит название закона Био-Савара- Лапласа. Из него следует, что напряженность направлена нор- мально к плоскости, проходящей через векторы d и r . В скалярной форме закон Био-Савара-Лапласа принимает вид:
| dH = | I d | sin α , | (3.85) |
| 4 π r 2 | |||
где α — угол между векторами d и r . Применим формулу (3.85) для вычисления напряженности поля линейного проводника бесконечной длины на расстоянии b от проводника (рис.). Перей- дем в формуле (3.85) от переменной d к переменной d α . Из рис. следует, что r = sin b α , d = sin rd α α = sin bd 2 α α . Подстав- ляя это в (3.85), получим, что вклад в величину напряженности поля выбранного элемента: dH = 4 π I r 2 sin α d α . Просуммировав вклады всех элементов тока от – ∞ до +∞, находим:
| H = | I | ∫ π sin α d α = | 2 I | . | (3.86) |
| 4 π b | 0 | 4 π b | |||
Величина H одинакова для всех точек, отстоящих от проводника на расстоянии b . Таким образом, силовые линии бесконечного линейного проводника представляют собой окружности, центры которых расположены на оси проводника. Следовательно, магнитное поле линейного проводника обладает цилиндрической симметрией.
Источник
Магнитное поле и его свойства
Магнитное поле это материя, которая возникает вокруг источников электрического тока, а также вокруг постоянных магнитов. В пространстве магнитное поле отображается как совокупление сил, которые способны оказать воздействие на намагниченные тела. Это действие объясняется наличием движущих разрядов на молекулярном уровне.
Магнитное поле формируется только вокруг электрических зарядов, которые находятся в движении. Именно поэтому магнитное и электрическое поле являются, неотъемлемыми и вместе формируют электромагнитное поле. Компоненты магнитного поля взаимосвязаны и воздействуют друг на друга, изменяя свои свойства.
Свойства магнитного поля:
1. Магнитное поле возникает под воздействие движущих зарядов электрического тока.
2. В любой своей точке магнитное поле характеризуется вектором физической величины под названием магнитная индукция, которая является силовой характеристикой магнитного поля.
3. Магнитное поле может воздействовать только на магниты, на токопроводящие проводники и движущиеся заряды.
4. Магнитное поле может быть постоянного и переменного типа
5. Магнитное поле измеряется только специальными приборами и не может быть воспринятым органами чувств человека.
6. Магнитное поля является электродинамическим, так как порождается только при движении заряженных частиц и оказывает влияние только на заряды, которые находятся в движении.
Размер магнитного поля зависит от скорости изменения магнитного поля. Соответственно этому признаку существуют два вида магнитного поля: динамичное магнитное поле и гравитационное магнитное поле. Гравитационное магнитное поле возникает только вблизи элементарных частиц и формируется в зависимости от особенностей строения этих частиц.
Магнитный момент возникает в том случае, когда магнитное поле воздействует на токопроводящую раму. Другими словами, магнитный момент это вектор, который расположен на ту линию, которая идет перпендикулярно раме.
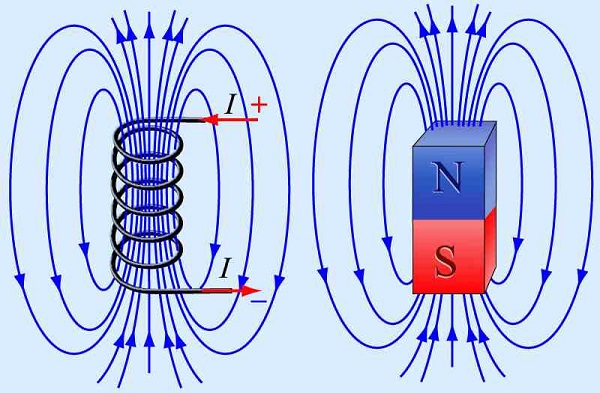
Магнитное поле можно изобразить графически с помощью магнитных силовых линий. Эти линии проводятся в таком направлении, так чтобы направление сил поля совпало с направлением самой силовой линии. Магнитные силовые линии являются непрерывными и замкнутыми одновременно.
Направление магнитного поля определяется с помощью магнитной стрелки. Силовые линии определяют также полярность магнита, конец с выходом силовых линий это северный полюс, а конец, с входом этих линий, это южный полюс.
Очень удобно наглядно оценить магнитное поле с помощью обычных железных опилок и листка бумаги.
Если мы на постоянный магнит положим лист бумаги, а сверху насыпим опилок, то частички железа выстроятся соответственно силовым линиям магнитного поля.
Направление силовых линий для проводника удобно определять по знаменитому правилу буравчика или правилу правой руки. Если мы обхватим проводник рукой так, чтобы большой палец смотрел по направлению тока(от плюса к минусу), то 4 оставшиеся пальцы покажут нам направление силовых линий магнитного поля. 
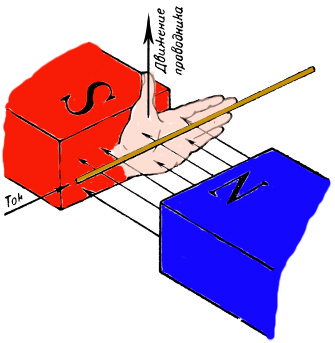
А направление силы Лоренца — силы, с которой действует магнитное поле на заряженную частицу или проводник с током, по правилу левой руки.
Если мы расположим левую руку в магнитном поле так, что 4 пальца смотрели по направлению тока в проводнике , а силовые линии входили в ладонь, то большой палец укажет направление силы Лоренца, силы действующей на проводник помещенный в магнитное поле.
На этом собственно всё. Появившиеся вопросы обязательно задавайте в комментариях.
Заметка: учите инглиш? — рейтинг школ английского языка (http://www.schoolrate.ru/) будет вам полезен при выборе.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник