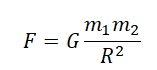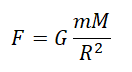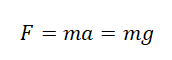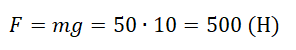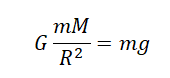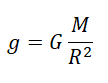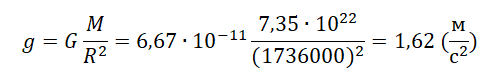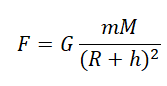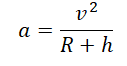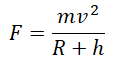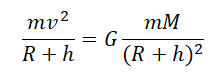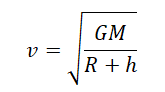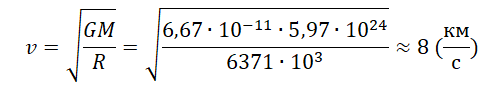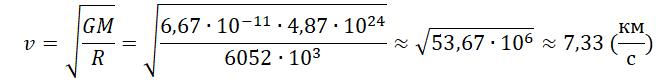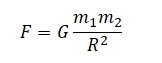Природа ускорения силы тяжести

Ускорение силы тяжести

Закон силы тяжести Замечание 1 Сила тяжести является одним из случаев проявления действия гравитационных.
ускорение свободного падения.
$ Сила тяжести имеет определенный вектор распространения.
силы тяжести.
вертикально вес будет отличаться от силы тяжести, исходя из вектора ускорения.

Анализ гравиметрических измерений ускорения силы тяжести

В данной работе приводится анализ первых гравиметрических измерений на территории бывшего Туркестана. Отмечается роль классических гравиметров при определении ускорения силы тяжести. На основе полевых измерений установлена гравиметрическая связь с Пулковской астрономической обсерваторией и Потсдамским телеграфным центром. Отмечается роль статических гравиметров, которые позволяют измерять разности ускорений силы тяжести на пунктах геодезической сети. В статье приводится традиционная модель, представляющая нормированные коэффициенты Cnm, Snm разложения потенциала силы тяжести по сферическим функциям. Перспективы использования спутниковых гравиметрических измерений изложены в работе.

Сила тяжести, формулы

Понятие силы тяжести Замечание 1 Сила тяжести $mg$ считается состоящей из гравитационного притяжения.
Сила тяжести сообщает всем телам, в независимости от их массы, равное ускорение, представляя при этом.
телу силой тяжести, обозначенное как ускорение свободного падения.
$ – ускорение силы тяжести, принуждающее тела стремиться друг к другу.
В задачах, связанных с задействованием ускорения свободного падения, такое ускорение обозначают буквой

Вычисления нормального ускорения силы тяжести вне эллипсоида

Представлены формулы А.В. Елагина, предназначенные для вычисления нормального ускорения силы тяжести вне эллипсоида. Тестирование производилось путём сравнения с результатами вычислений по формулам Сомильяна, В.Ф. Еремеева М.И. Юркиной и Ю.В. Сурнина. Разности ускорений, вычисленные по разным формулам не превышают 0.05 мкГал на высотах до 7500 м.

Источник

Гравитационные силы. Закон всемирного тяготения. | теория по физике 🧲 динамика

Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.

Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.

Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.

F — сила всемирного тяготения, m₁ и m₂ — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10 –11 Н ∙ м 2 /кг 2 ).

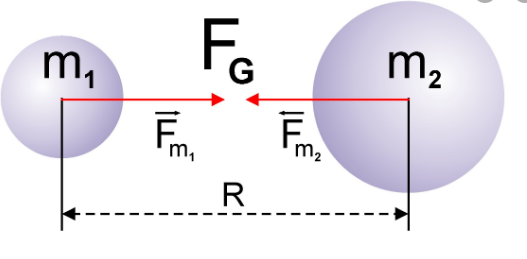
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.

Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m₁ = 1 кг и m₂ = 1 кг, то F = G.

Сила тяжести

Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.

Сила тяжести — сила, с которой Земля притягивает к себе тела.

Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле

Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:

Вывод формулы ускорения свободного падения

Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.

Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.

Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:

Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:

Формула расчета ускорения свободного падения

Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.

Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10 22 кг.

Переведем километры в метры: 1736 км = 1736000 м.

Первая космическая скорость

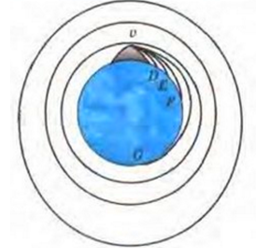
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

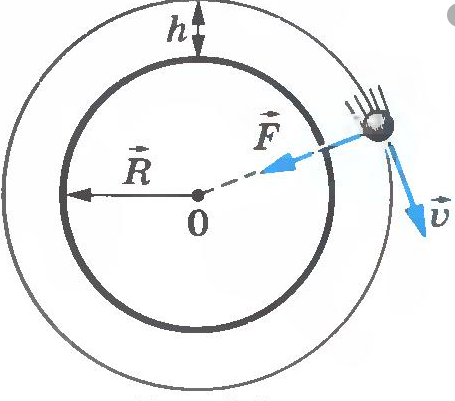
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.

Задание EF18521 Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).

Алгоритм решения

1. Записать исходные данные.
2. Записать закон всемирного тяготения.
3. Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
4. На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.

• Расстояние между двумя шарами в первом случае: R₁ = 2 м.
• Расстояние между двумя шарами во втором случае: R₂ = 6 м.
• Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.

Запишем закон всемирного тяготения:

Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m₁ и m₂.

R₂ больше R₁ втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

Алгоритм решения

Источник

Ускорение силы тяжести

Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Жэ» или «Жи»), — ускорение, сообщаемое телу под действием притяжения планеты или другого астрономического тела в безвоздушном пространстве — вакууме. Его значение для Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчетах обычно принимают g = 9,81 м/с².

Ускорение свободного падения на поверхности некоторых небесных тел, м/с 2

Луна	1,62	Сатурн	9,74
Меркурий	3,68 — 3,74	Земля	9,81
Марс	3,86	Нептун	11,0
Уран	7,51	Юпитер	23,95
Венера	8,88	Солнце	273,1

Значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.

Реальное ускорение свободного падения на поверхности Земли зависит от широты и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах [1] . Оно может быть вычислено по эмпирической формуле:

g = 9,780327(1 + 0,0053024sin 2 (φ) − 0,0000058sin 2 (2φ)) ,

где φ — широта рассматриваемого места. [2]

Вычисление ускорения свободного падения

Гравитационное ускорение на различной высоте h над Землёй

h, км	g, м/с 2	h, км	g, м/с 2
0	9.8066	20	9.7452
1	9.8036	50	9.6542
2	9.8005	80	9.5644
3	9.7974	100	9.505
4	9.7943	120	9.447
5	9.7912	500	8.45
6	9.7882	1000	7.36
8	9.7820	10 000	1.50
10	9.7759	50 000	0.125
15	9.7605	400 000	0.0025

Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центростремительного ускорения.

Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:

Термин жэ используется в космонавтике и авиации для обозначения перегрузок — увеличения веса тела, вызванного его ускоренным движением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 жи. Обычный человек может выдерживать перегрузки до 5 g. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при 2-3 g в глазах «краснеет» и человек теряет сознание из-за прилива крови к голове.

В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0g, но в таблице ниже этот же случай рассматривается как перегрузка в 1g. Похожий казус происходит при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме.

Примерные значения перегрузок, встречающихся в жизни

Человек, стоящий неподвижно	1 g
Пассажир в самолете при взлете	1,5 g
Парашютист при приземлении со скоростью 6 м/с	1,8 g
Парашютист при раскрытии парашюта (при изменении скорости от 60 до 5 м/с)	5,0 g
Космонавты при спуске в космическом корабле «Союз»	до 3,0—4,0 g
Летчик при выполнении фигур высшего пилотажа	до 5 g
Летчик при выведении самолета из пикирования	8,0—9 g
Перегрузка (длительная), соответствующая пределу физиологических возможностей человека	8,0—10,0 g
Наибольшая (кратковременная) перегрузка автомобиля, при которой человеку удалось выжить [3]	179,8 g

Примечания

Литература

Wikimedia Foundation . 2010 .

Источник