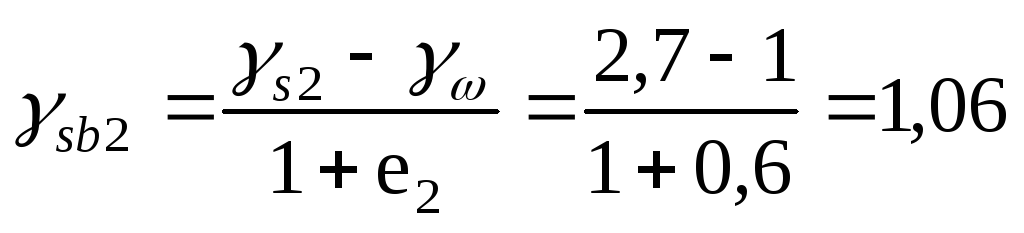Природное напряжение от собственного веса грунта

16. Распределение напряжений от собственного веса грунта

Напряжения от собственного веса грунта обычно называют природными (или «бытовыми») и существуют они всегда, независимо от застройки территории.

В грунтовом полупространстве, ограниченном сверху горизонтальной плоскостью z = 0, при горизонтальном напластовании грунтов можно считать, что напряжения зависят только от координаты z (глубины). Если в пределах толщины некоторого слоя грунта объемная масса γ постоянна, то вертикальные нормальные напряжения σ_z будут увеличиваться с глубиной и равны

σ_г= γh . (55)

Горизонтальные и вертикальные площадки являются главными, а горизонтальные нормальные напряжения σ_х и σ_y равны между собой. Горизонтальные смещения отсутствуют.

Исходя из предположения о линейной деформируемости грунта, по закону Гука, в этом случае имеем:

σ_z= ∑γ_i h_i (56)

Частицы грунта, залегающие ниже уровня грунтовых вод, испытывают взвешивающее действие воды (силу Архимеда), поэтому формула (50) будет иметь вид:

σ_г= ((γ_s—γ_w)/(1+e))h , (57)

где γ_s — удельный вес скелета грунта; γ_w — удельный вес воды; е — коэффициент пористости.

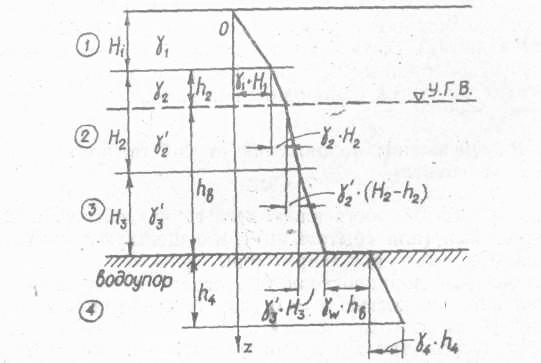
По В.А. Флорину, взвешивание имеет место для всех водонасыщенных грунтов, за исключением плотных глин, играющих роль водоупора. В связи с этим эпюра давления σ_z от собственного веса грунта на кровле водоупора имеет скачок (рис. 20), равный γ_wh_в, где h_в — расстояние от уровня грунтовых вод до кровли водоупора.

Рис. 20. Эпюра напряжений σ_г от собственного веса грунта

Горизонтальные напряжения от собственного грунта (см. п.7) можно найти по формуле

σ_x= γhξ = σ_zξ , (58)

где ξ — коэффициент бокового давления.

17. Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Общие положения. Распределение напряжений в основании в большой мере зависит от формы фундамента в плане. Поскольку в промышленном и гражданском строительстве обычно используются ленточные, прямоугольные или круглые фундаменты, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.

Напомним, что распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Полученные методами теории упругости напряжения соответствуют стабилизированному состоянию, т. е. такому периоду времени, когда все процессы консолидации и ползучести грунтов основания под действием приложенной нагрузки уже завершились и внешняя нагрузка оказывается полностью уравновешенной внутренними силами (эффективными напряжениями в грунте). Кроме того, принимается, что зоны развития пластических деформаций, возникающие в основании у краев фундамента (вследствие краевого эффекта), незначительны и не оказывают заметного влияния на распределение напряжений в основании.

Приведем общий ход решения задач о распределении напряжений в упругом полупространстве под действием местной нагрузки. В основе общего хода решения задач о распределении напряжений лежит решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885 г. Ж. Буссинеском. Это решение позволяет определить все компоненты напряжений и деформаций в любой точке полупространства М от действия силы Р (рис. 21, а). Поскольку для практических расчетов наибольшее значение имеют сжимающие напряжения, то их можно определить по следующей зависимости:

σ_z=(K/z 2 )P , (59)

K=(3/2π)×(1/((1+(r/z) 2 ) 5/2 .

Используя принцип суперпозиции, можно определить значение вертикального сжимающего напряжения в точке М при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 21, б)

σ_z=(K₁/z 2 )P₁+ (K₂/z 2 )P₂+…+ (K_n/z 2 )P_n (60)

а б

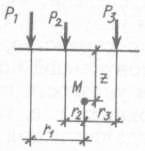
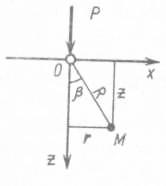
Рис. 21. Расчетная схема определения напряжений:

а – задача Буссинеска; б – при действии нескольких сосредоточенных сил

Используя приведенные выражения (59), (60), можно достаточно просто определить напряжения в любой точке основания при любой форме фундамента и заданном законе распределения нагрузки. Как правило, в гражданских и промышленных сооружениях фундаменты зданий имеют прямоугольную форму с шириной b и длиной l, если отношение (l/b)>10 то фундамент рассматривается как ленточный.

При расчетах напряжений под фундаментами зданий используют формулу

σ_z=αp, (61)

где α — коэффициент влияния; p — давление под подошвой фундамента.

Коэффициент влияния α зависит от параметров η=(l/b) и m=2z/b и определяют по таблицам [1] или приложению А.

Источник

Напряжения от собственного веса грунта

Вертикальные нормальные напряжения в грунте от веса лежащих выше грунтов называют природным или бытовым давлением и обозначают s_zg.

Природное давление в однородном грунте на глубине h определяются по формуле

где g – удельный вес грунта.

Природное давление в неоднородном основании на кровле (n +1)-го слоя вычисляется по формуле

где g_i и h_i – соответственно удельный вес и толщина i -го слоя грунта.

Удельный вес грунтов, залегающих ниже уровня подземных вод, но выше водоупора, должен приниматься с учетом взвешивающего действия воды по формуле (11). На кровлю водонепроницаемого слоя грунта (на водоупор) в этом случае действует дополнительное давление равное g_wh_w; здесь g_w = 10 кН/м 3 – удельный вес воды, h_w — разность отметок уровня грунтовых вод (WL) и кровли водоупора (рисунок 12).

Если под слоем водонепроницаемого грунта расположены грунтовые воды, то на кровлю грунта под водоупором действуют давления, уменьшенные на g_wh₂; здесь g_w = 10 кН/м 3 – удельный вес воды, h₂ – толщина водонепроницаемого слоя грунта (рисунок 13).

График напряжений от собственного веса грунта s_zg называется эпюрой напряжений от собственного веса грунта.

Пример 2. Построить эпюру напряжений от собственного веса грунта для грунтовых условий, приведенных на рисунке 14. Характеристики грунтов:

1 Слой — g₁ = 20 кН/м 3 ;

2 Слой — g_s = 26,6 кН/м 3 ; е = 0,661;

3 Слой — g₃ = 22 кН/м 3 .

Решение. На поверхности грунта напряжение от собственного веса грунта равно нулю.

Напряжение по подошве первого слоя равно s_{zg 1} = g₁h ₁ = 20×2 = 40 кПа.

Напряжение по подошве второго слоя вычисляем с учетом взвешивающего веса воды

Напряжение на кровле водоупора вычисляем с учетом дополнительного давления от веса воды во втором слое

Напряжение по подошве третьего слоя

Напряжение на кровле четвертого слоя вычисляем с учетом обратного скачка

Контрольные вопросы для самоподготовки.

1. Фазы напряженно-деформированного состояния грунтов при передаче на них постепенно увеличивающейся нагрузки.

2. Что характеризует начальное критическое давление?

3. Что понимают под расчетным сопротивлением грунта?

4. Как экспериментально определить распределение давлений по подошве фундамента?

5. Закон распределения давлений по подошве фундамента полученный в результате теоретических исследований.

6. Закон распределения давлений по подошве фундамента, применяемый в инженерных расчетах.

7. Определение напряжений в толще грунта от сосредоточенной силы, приложенной к поверхности грунтового основания.

8. Определение напряжений в толще грунта от равномерно распределенного давления, приложенной к поверхности грунтового основания на прямоугольной площади.

9. Какой принцип заложен в определении напряжений в толще грунта по методу угловых точек?

10. Какие имеются особенности определения напряжений в толще грунта от собственного веса при наличии в основании напорных и безнапорных грунтовых вод?

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

3. Определение напряжений в массиве грунта от действия собственного веса (бытовое давление)

На практике используют упрощенную методику расчета, основанную на предположении о том, что природные напряжения в массиве грунта формируются только под действием собственного веса [3  8]. Также принято считать, что все деформации массива от собственного веса прекратились и напряжения полностью стабилизировались. Практический интерес представляют значения сжимающих напряжений σ_z.

При горизонтальной поверхности массива грунта однородного напластования сжимающие напряжения на глубине z определяются выражением

,

где γ – удельный вес грунта.

Эпюра природных напряжений массива грунта однородного напластования при горизонтальной поверхности будет иметь вид треугольника (рис. 6 а).

При неоднородном напластовании или наличии подземных вод, а также при горизонтальной поверхности напряжения от собственного веса грунтов будут определяться отдельно для каждого слоя (рис. 6 б). Причем удельный вес грунта, расположенного ниже уровня подземных вод, будет определяться с учетом взвешивающего действия воды γ_sb:

,

где γ_s – удельный вес частиц грунта; γ_ω – удельный вес воды, принимается равным 1 т/м 3 ; е – коэффициент пористости грунта.

Рис. 6. Эпюры распределения напряжений от собственного веса грунтов

Если ниже уровня подземных вод залегает водоупорный слой, то на его кровле дополнительно учитывают давление от столба вышерасположенной воды равное γ_ω·h_ω (рис. 6 в).

Пример 6. Определить напряжения от собственного веса грунтов и построить эпюру распределения данных напряжений по скважине № 1. Исходные данные см. примеры 1 и 2.

Первоначально на основании данных инженерно-геологических изысканий (см. пример 2) строим в масштабе геологическую колонку с указанием мощности слоев грунта, уровней подземных вод и водоупора (рис. 7). Далее на основании результатов определения физико-механических характеристик грунтов (см. пример 1) для каждого слоя грунта указываем необходимые для дальнейшего расчета данные.

Рис. 7. Совмещенная схема геологической колонки и эпюры

распределения напряжений от собственного веса грунтов

Расчет напряжений от собственного веса грунтов проводим последовательно, начиная от поверхности земли. Расчетные точки располагаем на поверхности земли, на границах слоев грунтов, на уровнях подземных вод и водоупора.

На поверхности земли дополнительная пригрузка отсутствует, поэтому напряжение равно .

Напряжение на границе между первым и вторым слоями грунта определяем как сумму напряжений σ₁ и от собственного веса грунта первого слоя:

т/м 3 .

Напряжение на уровне подземных вод определяем как сумму напряжений σ₂ и от собственного веса грунта второго слоя на расстоянии от его кровли до уровня подземных вод:

т/м 3 .

Напряжение на границе между вторым и третьим слоями грунта определяем как сумму напряжений σ₃ и от собственного веса грунта второго слоя на расстоянии от уровня подземных вод до его подошвы, при этом учитываем взвешивающее действие воды на частицы грунта второго слоя

т/м 3 ,

где т/м 3 .

Напряжение на границе между третьим и четвертым слоями грунта определяем как сумму напряжений σ₄ и от собственного веса грунта третьего слоя, при этом учитываем взвешивающее действие воды на частицы грунта третьего слоя

т/м 3 ,

где т/м 3 .

На кровле четвертого слоя напряжение определяем с учетом дополнительного напряжения от столба вышерасположенной воды как сумму напряжений σ₅ и от собственного веса столба вышерасположенной воды:

т/м 3 .

На уровне нижней границы скважины напряжение определяем как сумму напряжений σ₆ и от собственного веса грунта четвертого слоя на расстоянии от его кровли до уровня забоя скважины:

т/м 3 .

Далее по полученным значениям σ₁–σ₇ в масштабе строим эпюру распределения напряжений от собственного веса грунтов, которую совмещаем с уже построенной геологической колонкой (рис. 7).

Источник