Птицефабрика реализует свою продукцию

1.3 Основные экономические показатели предприятия

Вывод: в соответствии с программой производства на 2010 год:

-темп роста объема производства продукции в сопоставимых ценах составил 118,9%;

— товарная продукция в действующих ценах выросла на 32952 млн. руб.;

-товары народного потребления выросли за 2010г. на 260440 млн. руб.;

-экспорт увеличился на 12983 млн. руб. по сравнению с 2009г.;

-выручка от реализации выросла на 39048 млн. руб.;

-стоимость реализованной продукции выросла на 29707 млн. руб.

1.4 Организация реализации готовой продукции

«Скидельская птицефабрика» реализует свою продукцию как на внутреннем, так и на внешнем рынках. На внутреннем рынке основной объём реализации продукции составляют тушки цыплят-бройлеров, полуфабрикаты из цыплят-бройлеров, колбасные изделия.

Продукция «Скидельской птицефабрики» реализуется практически во всех магазинах города Гродно, где созданы условия для реализации этой продукции, так как это продукция реализуется по сравнительно невысокой стоимости и пользуется большим спросом у населения в связи с хорошим качеством продукции. Договор купли-продажи и товарно-транспортная накладная – приложение В.

Информация о связях предприятия с организациями, которые являются заказчиками готовой продукции, изложена в следующей таблице:

Таблица 1.2 – Реализация готовой продукции

Наименование организации заказчика

Удаленность предприятия от заказчика

Способ транспортирования готовой продукции

Источник

Птицефабрика реализует свою продукцию

Рис. 5. Оптимальный ассортимент

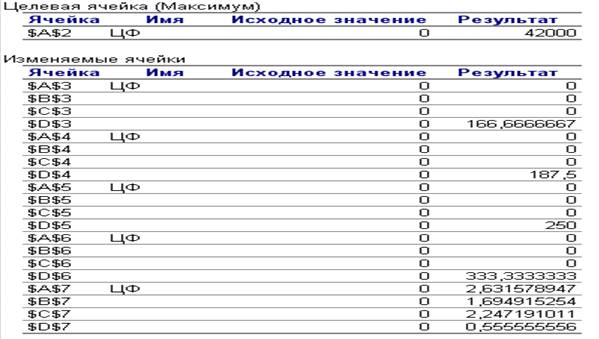
Рис. 6. Отчет по результатам

В отчете по результатам содержатся оптимальные значения переменных Х; значения целевой функции и левые части ограничений.

Отчет по устойчивости приводится на рис. 7.

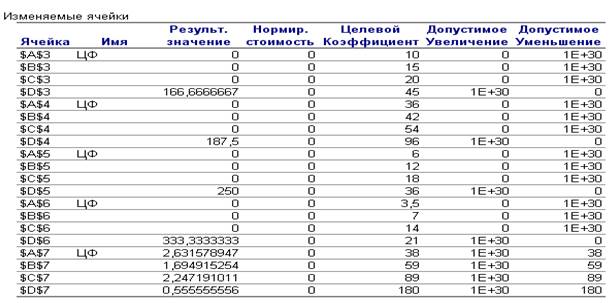
Первая часть таблицы содержит информацию, относящуюся к переменным:

– Результаты решения задачи.

– Нормированная стоимость, которая показывает, насколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. В данной задаче нормированная стоимость равна нулю.

– Коэффициенты целевой функции.

– Предельные значения целевых коэффициентов, при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на окорочка из индейки практически не ограничено, а допустимое уменьшение равно нулю. Это означает, что если цена уменьшится, то оптимальное решение изменится.

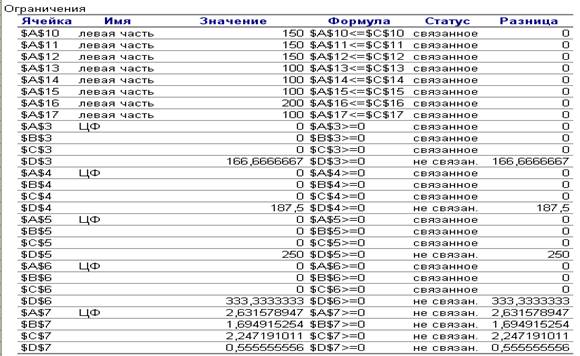
Во второй части содержится информация, относящаяся к ограничениям:

– Величина использованных ресурсов в колонке Результ. Значение.

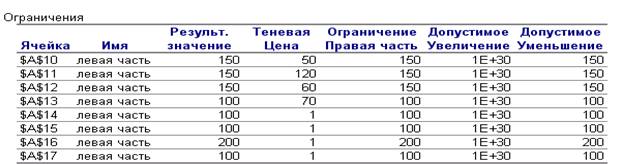
– Предельные значения приращения ресурсов. В графе Допустимое уменьшение показано, насколько можно уменьшить (устранить излишек) или увеличить ресурс, сохранив при этом оптимальное решение. Например, для окорочков допустимое увеличение не ограничено, а допустимое уменьшение имеет смысл не более, чем на 150 кг .

– Теневая цена показывает, насколько изменится ЦФ при изменении запаса ресурсов на одну единицу. Ценность дополнительной единицы продукции («теневая цена») рассчитывается только для дефицитных ресурсов. В данной задаче дефицитными, то есть сдерживающими рост ЦФ, являются все ресурсы. Они полностью используются в оптимальном плане.

Рис. 7. Отчет по устойчивости

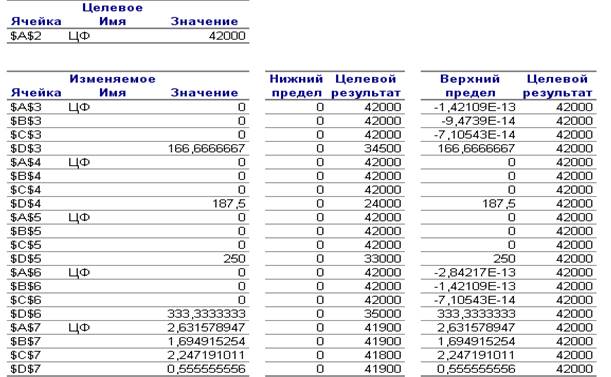
В отчете по пределам (рис.8) указаны значения ЦФ на верхних и нижних пределах значений переменных Х.

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Числовые данные для решения содержатся ниже в матрице планирования.

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

Источник

Две задачи по ЭММ и ПМ

В обработку поступили две партии досок для изготовления комплектов из трех деталей (треугольные каркасы настилов на стройплощадку), причем, вторая содержит 200 досок длиной по 4 м каждая. Каждый комплект состоит из двух деталей по 2 м каждая и одной детали в 1,25 м.

Ставится задача поиска рационального варианта раскроя поступившего в обработку материала

2. Экономико-математическая модель задачи

Критерием оптимальности в данной задаче является «максимум выпуска комплектной продукции». Обозначим через х_ij – количество деталей распиленного из досок i-ой партии для j – ой детали.

С учетом того, что треугольные каркасы из условия являются равнобедренными, целевая функция имеет вид:

f(x) = х₁₃ + х₂₃ ® max

х₁₁ + х₂₁ = х₁₂ + х_{22 —} условие равнобедренного треугольника

х₁₁ + х₂₁ = х₁₃ + х₂₃ — условие полной комплектации изделия – треугольник (количество ребер должно соответствовать количеству оснований треугольника)

Ограничения:

2х₁₁ + 2х₁₂ + 1,25х₁₃ ≤ 6,5*52 – ограничение по длине досок первой партии

2х₂₁ + 2х₂₂ + 1,25х₂₃ ≤ 4*200 – ограничение по длине досок во второй партии

Транспортная задача

1. Постановка экономической задачи (исходные данные варианта)

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Числовые данные для решения содержатся ниже в матрице планирования.

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки
2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

Источник

Задача — птицефабрика реализует свою продукцию

Птицефабрика реализует свою продукцию в собственной сети магазинов. В реализацию поступают как курицы различных категорий и индейки целиком, так и разделанные по частям. Вес отдельных частей и стоимость всего ассортимента продукции представлены в следующей таблице:

Курицы 1 категории, в них, кг.:

Курицы 2 категории, в них, кг.:

Стоимость одного изделия целиком, руб.

Известно, что в течение дня объемы спроса ограничены следующими значениями:

Составить оптимальный ассортимент продукции, при котором объем реализации ограничен возможным спросом, а стоимость всей продукции максимальна.

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

Похожие работы

• Решение задач линейного программирования с использованием Excel
• Три задачи по ЭММ и ПМ с решением
• Задача — компания, занимающаяся ремонтом автомобильных дорог
• Фермер отвел три земельных массива размером 5000, 8000 и 9000 га
• Задачи к экзамену по ЭММ и ПМ
• Задача металлургическому заводу требуется уголь
• Решение трех задач по ЭММ и ПМ
• Задачи к экзамену по ЭММ и ПМ с решением в excel
• Две задачи по ЭММ и ПМ
• Задачи с решением по экономико-математическим методам и прикладным моделям
• Экзаменационыые задачи по ЭММ и ПМ за 2007/2008г. с решением
• Оптимизационные экономико-математические модели (решение задач)
• Оптимизационные экономико-математические модели. Методы получения оптимальных решений
• Лабораторная работа по ЭММ и ПМ
• Задача о назначениях
• Экзаменационные задачи с решением в Excel по ЭММ и ПМ
• Задача о назначениях решение в Excel вариант 7
• Примеры решения задач в Excel по ЭММ и ПМ
• Решение задач по ММ и ПМ в Excel
• Решение задачи с помощью модели межотраслевого баланса

Источник