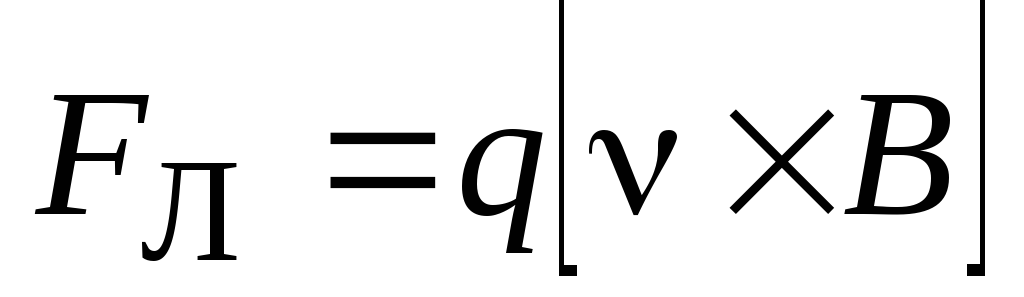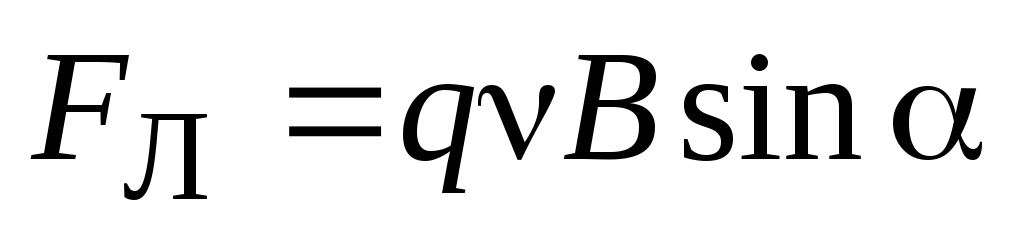3. Магнетизм
Опыт показывает, что вокруг движущегося заряда, наряду с электрическим полем, существует еще одна форма материи – магнитное поле. Магнитное поле и проявляет себя по действию, опять таки, на движущиеся заряды. Если действие электрического поля на заряженную частицу не зависит от ее скорости, то действие магнитного поля пропорционально скорости частицы. Но скорость – величина относительная! Значит в различных инерциальных системах отсчета величины магнитной и электрической сил, действующих на заряженную частицу, будут разными. Например, в системе отсчета, где частица покоится, действие магнитного поля вообще сведется к нулю, на частицу будет действовать одно только электрическое поле. Суммарное же действие полей (равнодействующая сила) на частицу одинаково в различных инерциальных системах отсчета. Это соответствует принципу относительности Эйнштейна: все явления природы в различных инерциальных системах отсчета происходят одинаково. В частности, независимо от инерциальной системы отсчета, тело должно испытывать одно и то же воздействие со стороны окружающих полей и тел. Эту силу называют электромагнитной силой, поскольку она состоит из двух составляющих – электрической и магнитной. Итак, электрические и магнитные силы – две части одного и того же явления – электромагнитного взаимодействия зарядов.
Характеристикой магнитного поля является вектор магнитной индукции 

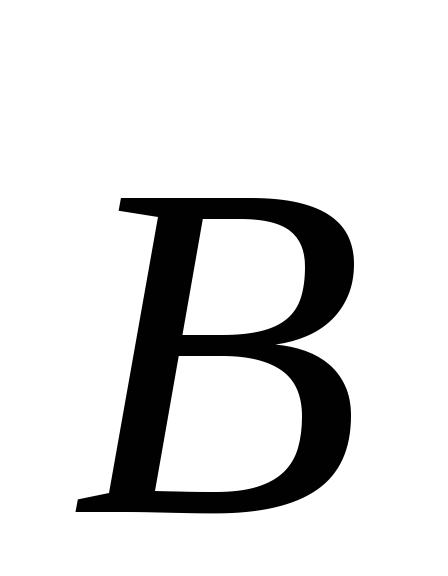
Изучение магнитных явлений мы начнем с сил, действующих со стороны магнитного поля на движущиеся заряды и токи. Далее будут обсуждаться источники магнитного поля и методы расчета вектора магнитной индукции.
Итак, сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, называется силой Лоренца. Эта сила определяется следующим выражением:
, (3.1)
где 
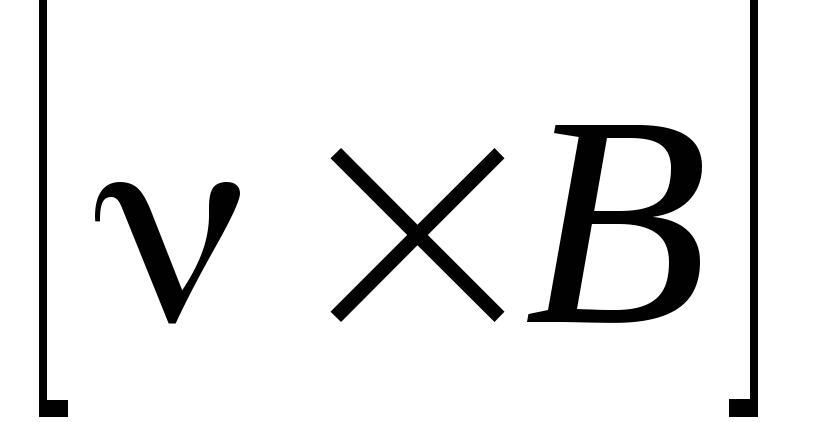
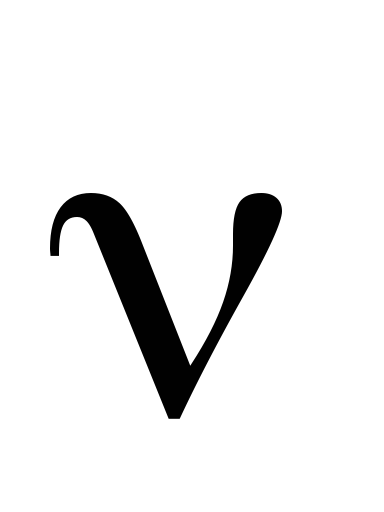
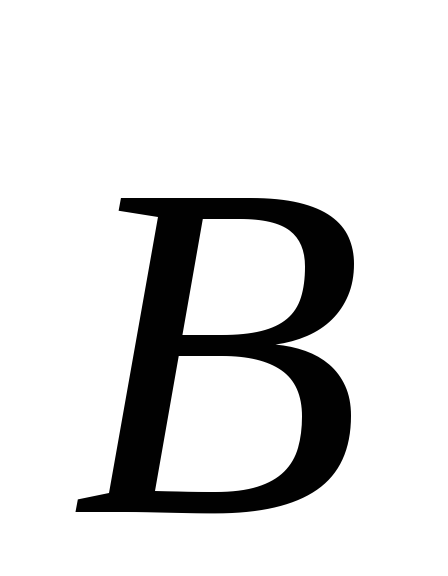
(3.1,а)
где 
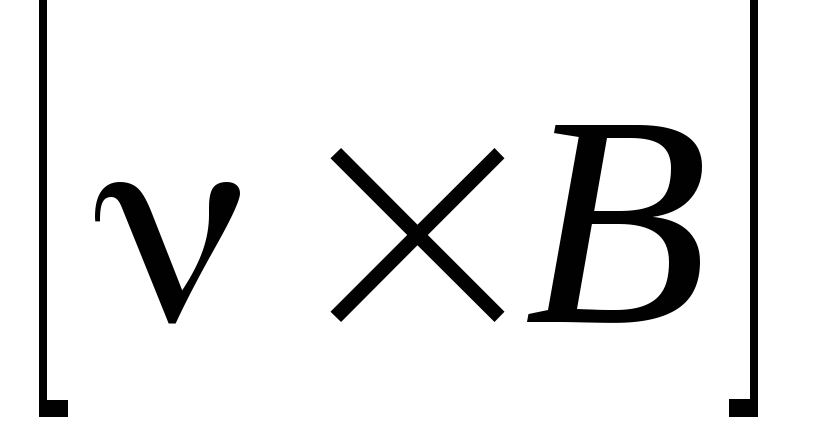
Говоря о различных по своей природе силах, важно знать особенности, связанные с расчетом работы, совершаемой этими силами. Учитывая эти особенности, удается классифицировать силы. Кроме того, работа теснейшим образом связана с энергией и всегда совершается за счет какого-то ее запаса, поэтому умение рассчитывать работу позволяет судить об энергетических превращениях.
Вспомним, например, что работа гравитационных и кулоновских сил не зависит от формы траектории тел или пути перехода системы тел из одного состояния в другое. Этот факт дает возможность рассматривать важнейшую физическую величину, называемую потенциальной энергией. Сами же силы называют потенциальными.
К классу диссипативных сил относят силы, полная работа которых всегда отрицательна. Это силы трения, сопротивления. Результатом действия этих сил является переход механической энергии во внутреннюю, другими словами, выделение тепла. Причем, количество выделившегося тепла по величине равно работе диссипативных сил.
Поскольку сила Лоренца перпендикулярна скорости заряженной частицы, ее работа всегда равна нулю, независимо от того, как эта частица движется в магнитном поле. Действительно, элементарная работа, совершаемая на небольшом участке траектории 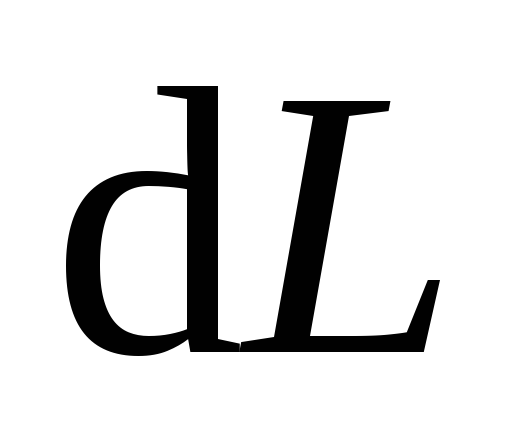
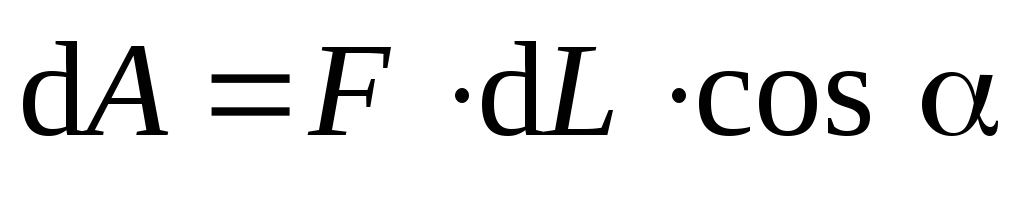




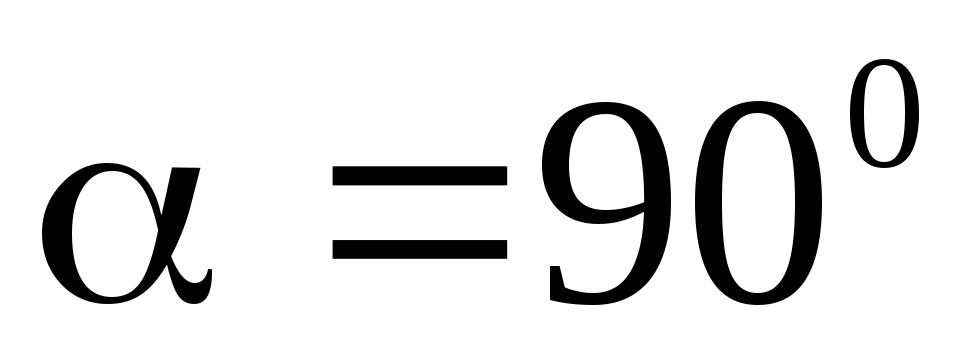
Обсуждаемое свойство силы Лоренца является уникальным. Подобных сил в природе больше не существует. Силы, работа которых всегда равна нулю, называют гироскопическими. В неинерциальных системах отсчета существуют и другие гироскопические силы, например, центробежная сила и сила Кориолиса. Эти силы фиктивны в том смысле, что невозможно указать тело, со стороны которого они действуют. К этим силам не применим третий закон Ньютона.
Источник
Сила Лоренца: определение, формула, применение на практике
Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10 -n Н, где 0
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Формула силы Лоренца при наличии магнитного и электрического полей
Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
Применение на практике
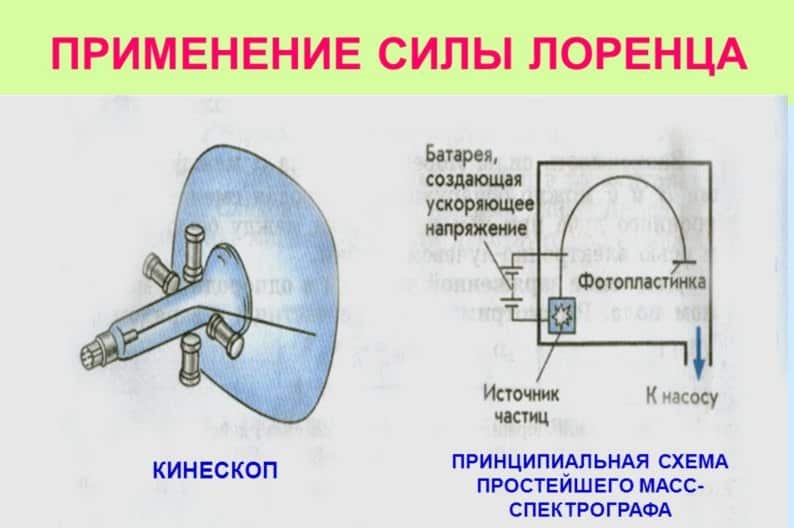
Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.
Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.
На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.
Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).
Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.
Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.
На основании действия силы Лоренца создано много других устройств, используемых на практике.
Источник