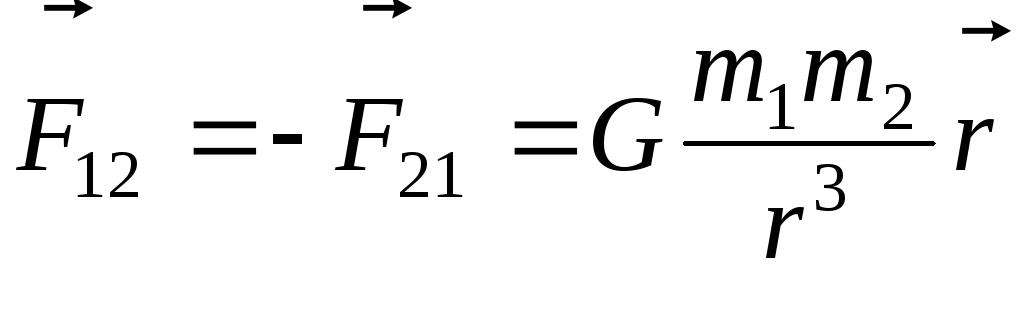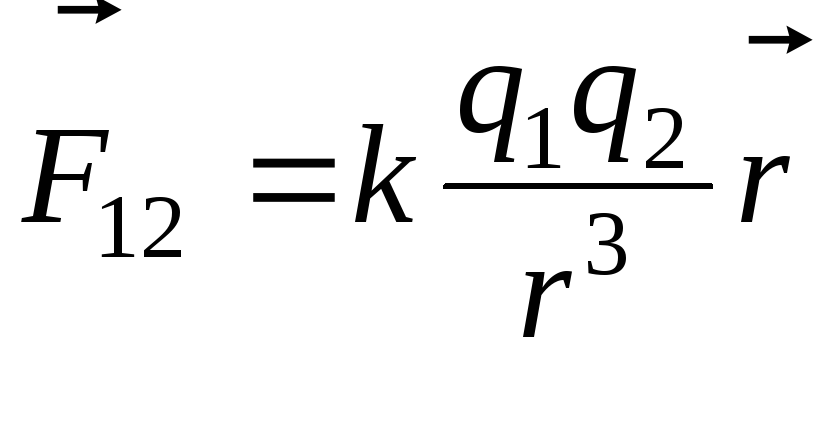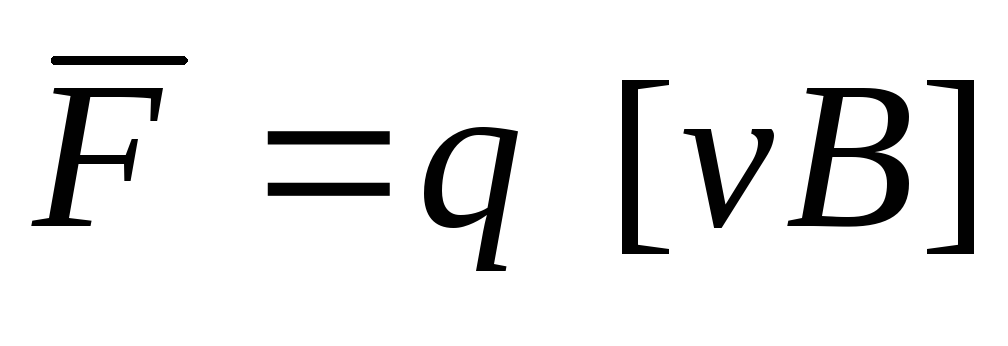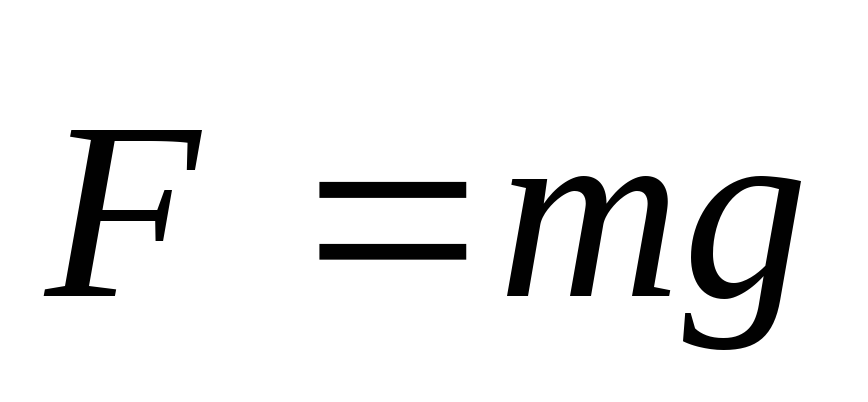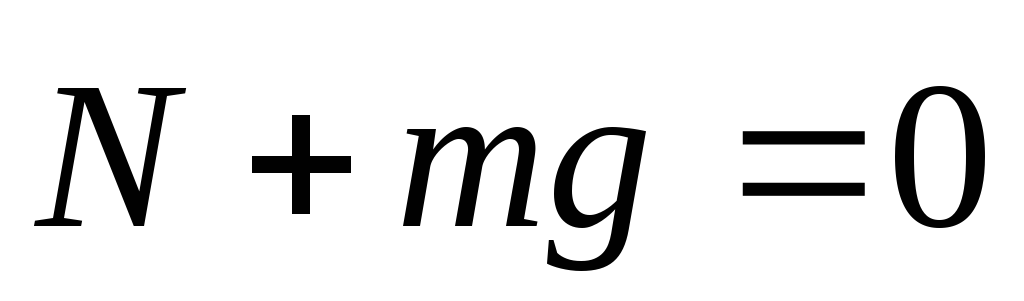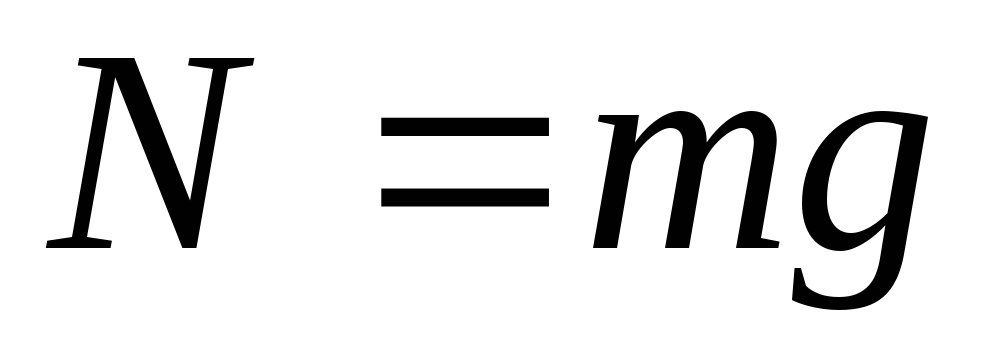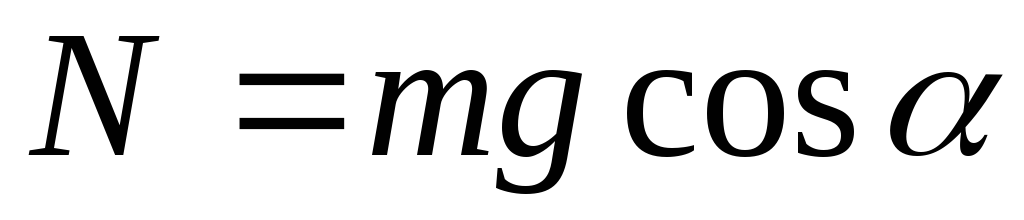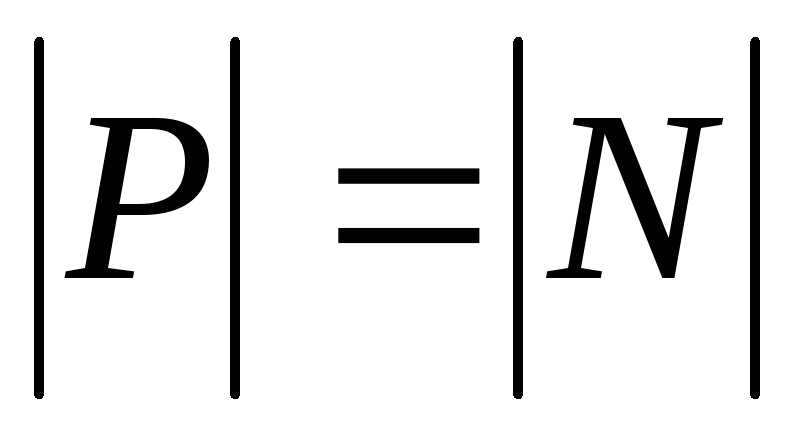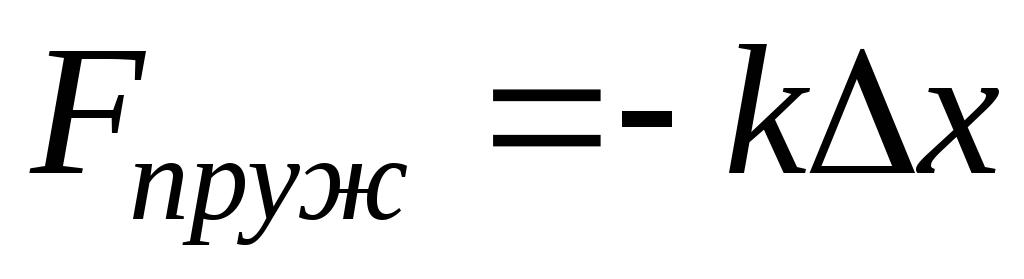Сила трения какая природа силы

10. Силы трения: природа сил трения; коэффициент трения скольжения; закон сухого трения; трение покоя; учёт и использование трения в быту и технике.

Сила трения покоя препятствует возникновению движения одного тела по поверхности другого.

Скольжения- если тело скользит.

Качения- действует на катящиеся тела, возникает из-за деформации поверхности перед катящимся телом.

Природа сил трения- электромагнитная. Это значит, что причиной ее возникновения являются силы взаимодействия между частицами, из которых состоит вещ-во. 2-я причина возникновения сил трения-шероховатые поверхности.

Коэффициент трения- количественная хор-ка силы, необходимая для скольжения или движения одного материала по поверхности другого.

38.Трансформатор.

Электрический ток получил широкое применение, потому что его можно преобразовать почти без потерь.

Электрические станции преобразуют электрический ток высоко напряжения в электрический ток низкого напряжения, который используется в промышленности.

Трансформатор- устройство, преобразующее переменный ток, при котором напряжение может увеличиваться или уменьшаться в несколько раз практически без потерь мощности.

1878г- Яблочков: первый трансформатор.

1. Стальной сердечник
2. Первичная катушка(подключена к источнику переменного тока)
3. Вторичная катушка(подключена к нагрузке)

Принцип действия(в основе явления электромагнитной индукции):

Сердечник концентрирует магнитное поле, которое существует практически только внутри сердечника и одинаково во всех его сечениях.

N₁— кол-во витков в первой катушке

N₂— кол-во витков во второй катушки

т.к активное сопротивление обмотки трансформатора стремится к нулю, модуль напряжения катушки приблизительно равен модулю ЭДС в этой катушке. | u_1|~|e₁|

II. а) Сила тока равна нулю, цепь разомкнута

ЭДС1,ЭДС2 изменяются синфазно, поэтому их мгновенные значения можно заменить действующими значениями.

Если коэффициент(к)меньше 1, то трансформатор повышающий, а если больше 1, то понижающий.

б) Сила тока не равна нулю, цепь замкнута.

Если вторичная обмотка замкнута, то изменяется магнитный поток. Согласно правилу Ленца магнитный поток должен уменьшать ЭДС индукции в первой обмотке, но это невозможно, т.к модуль направления на зажимах первой катушки приблизительно равен ЭДС первой катушки, поэтому при замыкании второй обмотки сила тока в первой обмотке возрастает.

Во столько раз повышаем напряжение, во столько раз уменьшаем силу тока.

Как можно избежать потери энергии:

1. Уменьшить силу тока
2. Увеличить площадь поперечного сечения проводника. Это приведет к возрастанию расхода материала алюминия и меди и как следствие должно привести к увеличению массы опор, которые удерживают проводники, т.е к удорожанию строительства линий электропередач(ЛЭП)

Все это ЭЛЕКТРИЧЕСКИЕ ЭНЕРГИИ.

Свойства электроэнергий:

1. легко превращаются в другие виды
2. легко передавать на большие расстояния без потерь
3. просто с высоких КПД преобразовать напряжение и дробить на порции
4. не наносит вред окружающей среде

Передача электроэнергии:

С электростанций электроэнергия поступает в повышающий трансформатор, оттуда по ЛЕП поступает в понижающий трансформатор1, оттуда во второй, в третий и отсюда к потребителю.

Источник

Природа сил

Все известные взаимодействия и соответственно силы в природе сводятся к следующим четырем типам: гравитационное, электромагнитное, сильное, слабое.

Гравитационное взаимодействие свойственное всем телам во Вселенной, проявляется в виде взаимного притяжения всех тел в природе, независимо от среды в которой они находятся, в микромире элементарных частиц при обычных энергиях роли не играет. Ярким примером является притяжение Землей. Это взаимодействие подчиняется закону всемирного тяготения: сила взаимодействия между двумя материальными точками массами m₁ и m₂ прямо пропорциональная произведению этих масс и обратно пропорциональная квадрату расстояния между ними. Математически этот закон имеет вид:

(3.7)

где G = 6,67 10 -11 Н м 2 /кг 2 — гравитационная постоянная, которая определяет силу притяжения между двумя одинаковыми телами с массами m₁ = m₂ = 1 кг на расстоянии r = 1 м.

Электромагнитное взаимодействие – взаимодействие между неподвижными и подвижными электрическими зарядами. Этим взаимодействием в частности обусловлены силы межмолекулярного и межатомного взаимодействия.

Взаимодействие между двумя точечными неподвижными зарядами q₁ и q₂ подчиняется закону Кулона:

,

где k = 9 10 9 Н м 2 /Кл 2 – коэффициент пропорциональности.

Если заряд движется в магнитном поле, то на него действует сила Лоренца:

v – скорость заряда, В – вектор магнитной индукции.

Cильное взаимодействие обеспечивает связь нуклонов в ядре атома. Слабое отвечает за большинство распадов элементарных частиц, а также за процессы взаимодействия нейтрино с веществом.

В классической механике мы имеем дело с гравитационными и электромагнитными силами, которые приводят к появлению сил притяжения, сил упругости, сил трения и других.

Сила тяжести характеризует взаимодействие тела с Землей.

Вблизи Земли все тела падают приблизительно с одинаковым ускорением g  9,8 м/с 2 , которое называется ускорением свободного падения. Отсюда следует, что вблизи Земли на каждое тело действует сила тяжести, которая направлена к центру Земли и равна произведению массы тела на ускорение свободного падения.

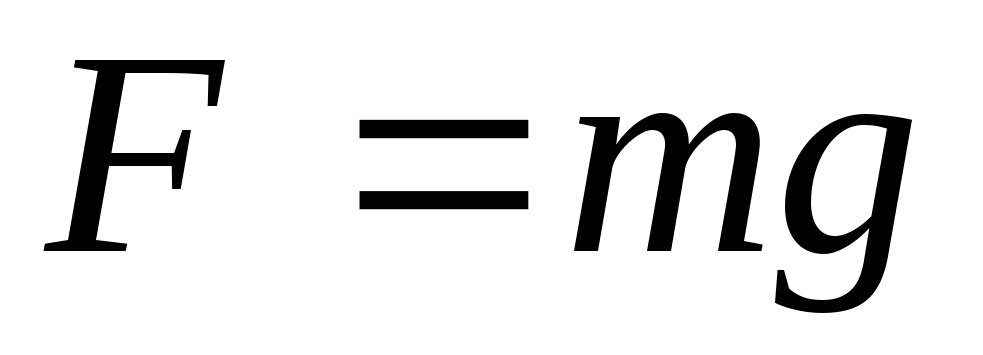
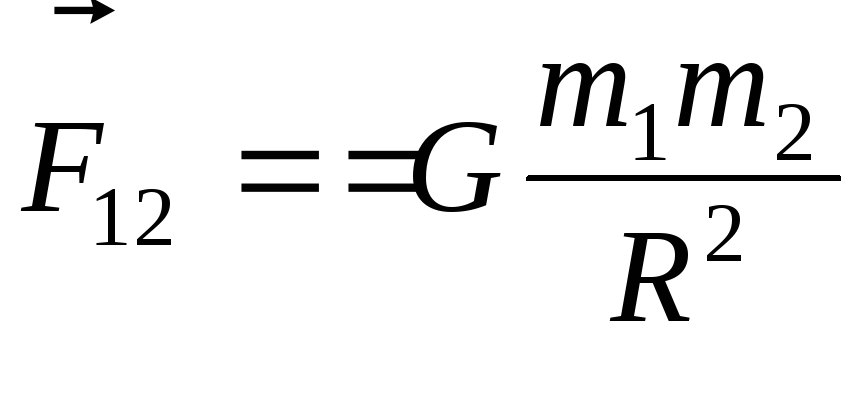
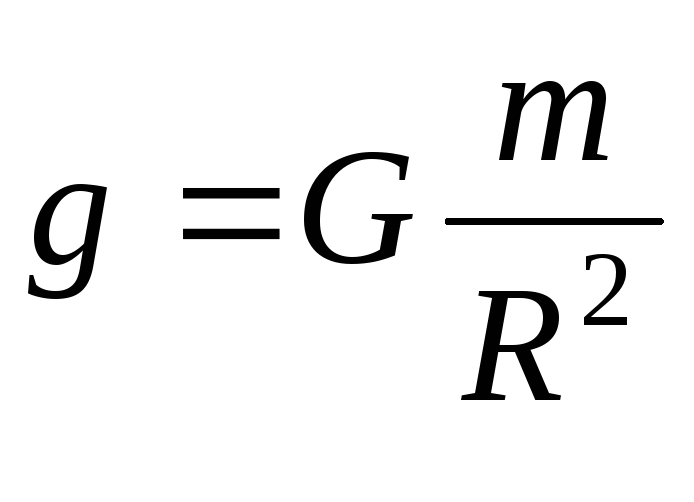
вблизи поверхности Земле поле однородно (g=const). Сравнивая с, получим, что.

Сила реакции опоры – сила , с которой опора действует на тело. Она приложена к телу и перпендикулярна поверхности соприкосновения. Если тело лежит на горизонтальной поверхности, то сила реакции опоры численно равна силе тяжести. Рассмотрим 2 случая.

Пусть тело покоится, тогда на него действует две силы. Согласно 2 закону Ньютона

Найдем проекции этих сил на ось у и получим, что

2. Пусть теперь тело находится на наклонной плоскости, составляющей угол с горизонтом (см. рис.).

Рассмотрим случай, когда тело будет покоиться, тогда на тело будут действовать две силы, уравнение движения выглядит аналогично первому случаю. Записав 2 закон Ньютона в проекции на ось у, получим, что сила реакции опоры численно равна проекции силы тяжести на перпендикуляр к этой поверхности

Вес тела – сила, с которой действует тело на опору или подвес. Вес тела равен по модулю силе реакции опоры и направлен противоположно

Часто путают силу тяжести и вес. Это обусловлено тем, что в случае неподвижной опоры эти силы совпадают по величине и по направлению Однако надо помнить, что эти силы приложены к разным телам: сила тяжести приложена к самому телу, вес приложен к подвесу или опоре. Кроме того, сила тяжести всегда равна mg, независимо от того покоится тело или движется, сила веса зависит от ускорения, с которым движутся опора и тело, причем она может быть как больше, так и меньше mg, в частности, в состоянии невесомости она обращается в нуль.

Сила упругости. Под действием внешних сил может происходить изменение формы тела – деформация. Если после прекращения действия силы форма тела возобновляется, деформация называется упругой. Для упругой деформации справедлив закон Гука:

x — удлинение тела вдоль оси х, k — коэффициент пропорциональности, который называют коэффициентом упругости.

При непосредственном соприкосновении тел помимо сил упругости могут возникать силы и другого типа, так называемые силы трения.

Силы трения бывают двух видов:

1. Сила трения покоя.
2. Сила трения, обусловленная движением тел.

Сила трения покоя – сила, с которой действует поверхность на покоящееся на ней тело в направлении, противоположном приложенной к телу силе (см. рис) и равная ей по модулю Силы трения 2 типа появляются при перемещении соприкасающихся тел или частей друг относительно друга. Трение, возникающее при относительном перемещении двух соприкасающихся тел, называют внешним. Трение между частями одного и того же сплошного тела (жидкость или газ), носит название внутреннего.Сила трения скольжения действует на тело в процессе его перемещения по поверхности другого тела и равна произведению коэффициента трения  между этими телами на силу реакции опоры N и направлена в сторону, противоположную относительной скорости движения этого тела F = N Силы трения играют очень большую роль в природе. В нашей повседневной жизни трение нередко оказывается полезным. Например, затруднения которые испытывают пешеходы и транспорт во время гололедицы, когда трение между покрытием дороги и подошвами пешеходов или колесами транспорта значительно уменьшается. Не будь сил трения, мебель пришлось бы прикреплять к полу, как на судне во время качки, ибо она при малейшей негоризонтальности пола сползла бы в направлении покатости. Закон сохранения импульса Замкнутой (изолированной) системой тел называют такую систему, тела которой не взаимодействуют с внешними телами или если равнодействующая внешних сил равна нулю. Если на систему материальных точек не действуют внешние силы, то есть система изолирована (замкнутая), из (3.12) выплывает, что , или (3.13) Мы получили фундаментальный закон классической физики — закон сохранения импульса: в изолированной (замкнутой) системе суммарный импульс остается величиной постоянной. Для того, чтобы выполнялся закон сохранения импульса достаточно, чтобы система была замкнута. Закон сохранения импульса является фундаментальным законом природы не знающим исключений. В нерелятивистском случае можно ввести понятие центра масс (центра инерции) системы материальных точек, под которым понимают воображаемую точку, радиус-вектор которой , выражается через радиусы векторы материальных точек по формуле: (3.14) Найдем скорость центра масс в данной системе отсчета, взяв производную по времени от соотношения (3.14) . (3.14) Импульс системы равняется произведению массы системы на скорость ее центра инерции. . (3.15) Понятие центра масс позволяет придать уравнению другую форму, которая часто оказывается более удобной. Для этого достаточно учесть, что масса системы есть величина постоянная. Тогда (3.16) где – сумма всех внешних сил, которые действуют на систему. Уравнение (3.16) – уравнение движенияцентра инерции системы. Теорема о движении центра масс гласит: центр масс движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на систему. Если система замкнута, то . В этом случае уравнение (3.16) переходит в, из которого следуетV=const. Центр масс замкнутой системы движется прямолинейно и равномерно.

Источник