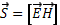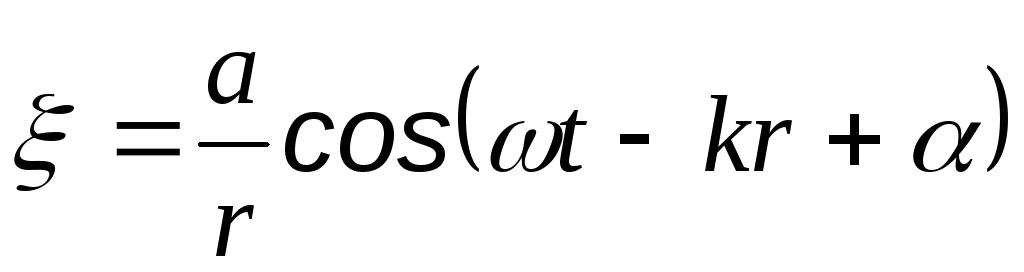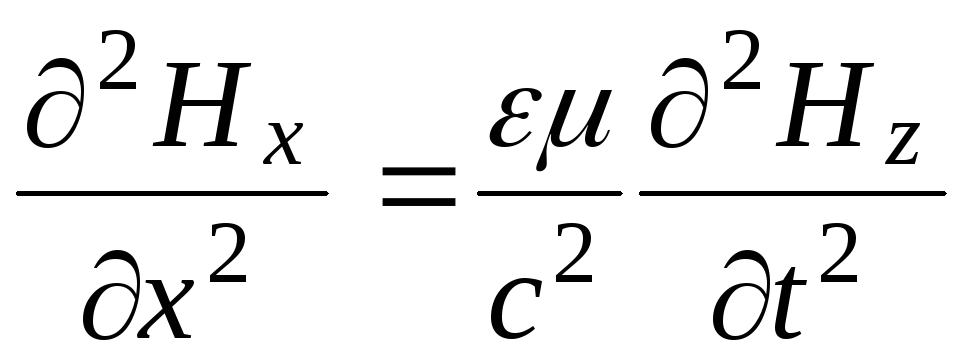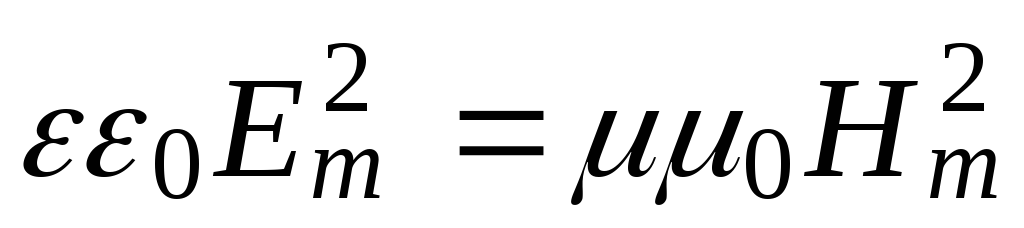Световая волна ее природа характеристики световой волны

Световая волна и её характеристики.

Оптика– это раздел физики, который изучает распространение света и взаимодействие его с веществом. Свет представляет собой электромагнитное излучение и обладает двойственной природой. В одних явлениях свет ведёт себя как электромагнитная волна, в других – как поток особых частиц фотонов или квантов света. Волновыми свойствами света занимается волновая оптика, квантовой – квантовая.

Свет– поток фотонов. С точки зрения волновой оптики световая волна – это процесс колебания электрического и магнитного полей, распространяющихся в пространстве.

Оптика занимается световыми волнами, в основном инфракрасного, видимого, ультрафиолетового диапазонов. Как электромагнитная волна свет обладает следующими свойствами (они следуют из уравнения Максвелла):

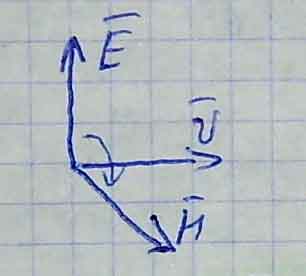
Вектора напряжённости электрического поля E, магнитного поляHи скорость распространения волныVвзаимно перпендикулярны и образуют правовинтовую систему.

Вектора EиHколеблются в одной фазе.

Для волны выполняется условие:

Уравнение световой волны имеет , где— волновое число,— радиус-вектор,— начальная фаза.

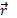
При взаимодействии световой волны с веществом наибольшую роль играет электрическая составляющая волны (магнитная составляющая вне магнитных средах влияет слабее), поэтому Eназываютсветовым вектором и его амплитудуобозначают А.

Уравнение (1) является решением волнового уравнения, которое имеет вид:

(2), где— лапласиан;V– фазовая скоростьV=c/n(3).

Для немагнитных сред =1 =>. Из (3) видно, чтоn=c/v. По виду волновой поверхности различают плоские, сферические, эллиптические и т.д. волны.

Для плоской волны амплитуда светового вектора уравнения (1) постоянна. Для сферического она уменьшается с расстоянием от источника по закону .

Перенос энергии световой волны характеризуется вектором Поинтига .

Он представляет собой плотность потока энергии и направлен по скорости – в сторону его переноса. Вектор Sочень быстро изменяется со временем, поэтому любой приёмник излучения, в том числе и глаз, в течение времени наблюдения, гораздо большего, чем период волны, регистрирует усреднённое по времени значение вектора Поинтига, которое называетсяинтенсивностью световой волны.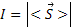, где . Учитывая (1) и то, что дляHоно имеет такой же вид, можно записать, что(4)

Если усреднить уравнение (4) по времени, то второе слагаемое исчезнет, тогда (5). Из (5) следует, чтоI-(6).

Интенсивность I– это количество энергии переносимое за единицу времени световой волной через единицу площади. Линию, по которой распространяется энергия волны, называетсялучом. Ещё одной характеристикой световой волны является поляризация. Реальный источник состоит из огромного числа атомов, которые излучают, будучи возбуждёнными, в теченииt=10 -8 c, испуская при этом обрывок волны λ=3м.

Эти волны имеют различные направления вектора Eв пространстве, поэтому в результирующем излучении за время наблюдения встречаются различные направления вектораE, т.е. направлениеEдля реального источника изменяется хаотически по времени, и свет от такого источника называетсяестественным (неполяризованным). Если же направление колебаний вектораEупорядочены, то такой свет –поляризованный. Различают свет плоско поляризованный, поляризованный по кругу и эллипсу.

Источник

Предварительные сведения

_{I пара или}

IIпара или

К уравнениям добавляют связи:

,

,

.

Под уравнением волны понимают уравнение вида , где— смещение точки с координатамиx,y,zв момент времениt.

Волна, у которой фронт волны и волновая поверхность являются плоскостями, называется плоской волной.

Её уравнение , где координатная осьXнаправлена по направлению распространения волны, то есть перпендикулярно волновым поверхностям.

.

Тогда в произвольном значении xколебания придут с запозданием:

Зафиксировав фазуи продифференцировав— получим скорость, с которой перемещается данное значение фазы – фазовая скорость.

Учитывая, что ,, уравнение волны примет вид:

где — волновое число.

Затухание плоской волны, как показа опыт, происходит по экспоненциальному закону

Для точечного источника амплитуда убывает с расстоянием ~1/rдаже в непоглощенной среде

где r– расстояние от точечного источника.

Для волны (плоской) распространяющейся в направлении под углами к осям x, y, zуравнение волны примет вид:

где — волновой вектор

Учитывая, что , уравнение плоской волны можно записать:

где — комплексное число, называемое комплексной амплитудой,.

Уравнение любой волны является решением дифференцированного уравнения, называемого волновым.

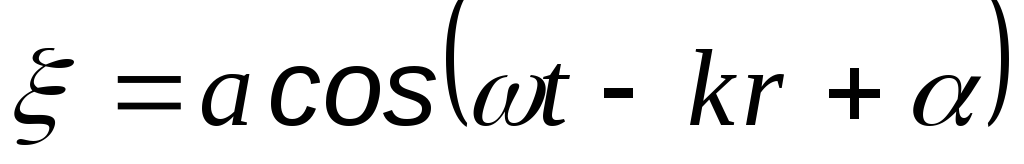
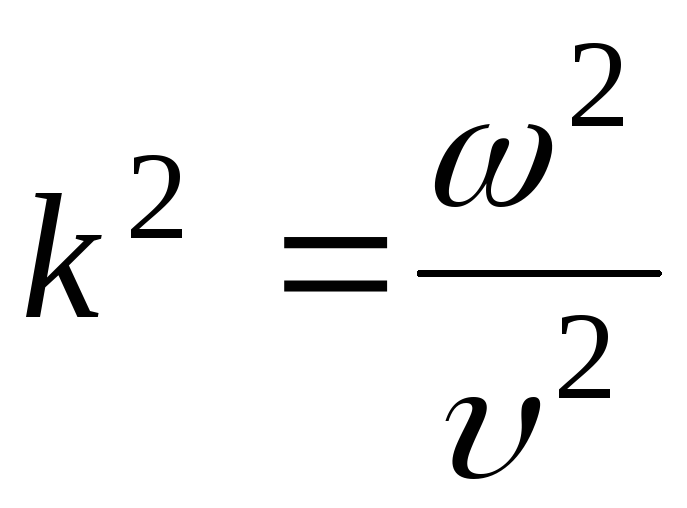
Если продифференцировать функцию дважды поx, y, z, t, сложить производные по координатам и учесть, что, получим уравнение, которое называют волновым

— волновое уравнение

Всякая функция, удовлетворяющая уравнению этого вида, описывает некоторую волну. Корень квадратный из величины, обратной коэффициенту придает фазовую скорость этой волны.

Световая волна. Основные характеристики световой волны

Развитие физики показало, что свет – сложное явление (волна, частица). Мы изучаем волновую оптику, которая описывает световые явления с точки зрения волновой природы света. Свет – это электромагнитная волна, то есть система вихревых электрических и магнитных полей взаимно порождающих друг друга.

Существование электромагнитных волн вытекает из уравнений Максвелла:

— оператор Гамильтона (2)

В случае однородной нейтральной и непроводимой среды j=0 и постояннымии:

Тогда уравнения (2) запишутся:

Взяв операцию ротор от первых двух уравнений, поменяв последовательность дифференцирования по координатам и по времени, с учетом оставшихся уравнений, получим уравнения:

(3)

Учтено, что .

Это и есть волновые уравнения, которое неразрывно связаны друг с другом, описывают некоторую волну, скорость которой (фазовая):

(3’)

В вакууме == 1,=с.

Рассматривая плоскую электромагнитную волну, распространяющуюся по направлению осиX(тогда компонентыне будут зависеть отyиz) и записывая уравнения Максвелла, получим, что векторыперпендикулярны, а волновые уравнения примут вид:

Векторы направлены вдоль взаимно перпендикулярных осейXиY.

Решением последних уравнений являются функции:

(4)

Для того, чтобы эти решения удовлетворяли уравнениям Максвелла, необходимо равенство начальных фаз₁ и₂и

(5)

Таким образом, колебания электрических и магнитных векторов в электромагнитных волнах происходят в одной фазе (₁ =₂), а амплитуды связаны соотношением

.

Моментальный снимок электромагнитных волн: векторы образуют правовинтовую систему с направлением распространения волны. В фиксированной точке пространства векторыизменяются по гармоничному закону. Уравнения (4) можно записать с учетом сказанного в векторном виде:

Источник

Световая волна и её характеристики.

Оптика – это раздел физики, который изучает распространение света и взаимодействие его с веществом. Свет представляет собой электромагнитное излучение и обладает двойственной природой. В одних явлениях свет ведёт себя как электромагнитная волна, в других – как поток особых частиц фотонов или квантов света. Волновыми свойствами света занимается волновая оптика, квантовой – квантовая.

Свет – поток фотонов. С точки зрения волновой оптики световая волна – это процесс колебания электрического и магнитного полей, распространяющихся в пространстве.

Оптика занимается световыми волнами, в основном инфракрасного, видимого, ультрафиолетового диапазонов. Как электромагнитная волна свет обладает следующими свойствами (они следуют из уравнения Максвелла):

Вектора напряжённости электрического поля E, магнитного поля H и скорость распространения волны V взаимно перпендикулярны и образуют правовинтовую систему.

Вектора E и H колеблются в одной фазе.

Для волны выполняется условие:

Уравнение световой волны имеет , где — волновое число, — радиус-вектор, — начальная фаза.

При взаимодействии световой волны с веществом наибольшую роль играет электрическая составляющая волны (магнитная составляющая вне магнитных средах влияет слабее), поэтому E называют световым вектором и его амплитуду обозначают А.

Уравнение (1) является решением волнового уравнения, которое имеет вид:

(2), где — лапласиан; V – фазовая скорость V=c/n (3).

Для немагнитных сред =1 => . Из (3) видно, что n=c/v. По виду волновой поверхности различают плоские, сферические, эллиптические и т.д. волны.

Для плоской волны амплитуда светового вектора уравнения (1) постоянна. Для сферического она уменьшается с расстоянием от источника по закону .

Перенос энергии световой волны характеризуется вектором Поинтига .

Он представляет собой плотность потока энергии и направлен по скорости – в сторону его переноса. Вектор S очень быстро изменяется со временем, поэтому любой приёмник излучения, в том числе и глаз, в течение времени наблюдения, гораздо большего, чем период волны, регистрирует усреднённое по времени значение вектора Поинтига, которое называется интенсивностью световой волны. , где . Учитывая (1) и то, что для H оно имеет такой же вид, можно записать, что (4)

Если усреднить уравнение (4) по времени, то второе слагаемое исчезнет, тогда (5). Из (5) следует, что I — (6).

Интенсивность I – это количество энергии переносимое за единицу времени световой волной через единицу площади. Линию, по которой распространяется энергия волны, называется лучом. Ещё одной характеристикой световой волны является поляризация. Реальный источник состоит из огромного числа атомов, которые излучают, будучи возбуждёнными, в течении t=10 -8 c, испуская при этом обрывок волны λ=3м.

Эти волны имеют различные направления вектора E в пространстве, поэтому в результирующем излучении за время наблюдения встречаются различные направления вектора E, т.е. направление E для реального источника изменяется хаотически по времени, и свет от такого источника называется естественным (неполяризованным). Если же направление колебаний вектора E упорядочены, то такой свет – поляризованный. Различают свет плоско поляризованный, поляризованный по кругу и эллипсу.

Источник