Свойства природы корпускулярно волнового дуализма

Глава 28 Элементы квантовой механики § 213. Корпускулярно-волновой дуализм свойств вещества

Французский ученый Луи де Бройль (1892—1987), осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой приро­де света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма.Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Итак, согласно де Бройлю, с каждым микрообъектомсвязываются, с одной сторо­ны,корпускулярныехарактеристики — энергияЕи импульсp, а с другой —волновые характеристики —частотаи длина волны.Количественные соотношения, связыва­ющие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

(213.1)

Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

(213.2)

Это соотношение справедливо для любой частицы с импульсом р.

Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. амери­канские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кри­сталла никеля, — дает отчетливую дифракционную картину. Дифракционные макси­мумы соответствовали формуле Вульфа — Брэггов (182.1), а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (213.2). В даль­нейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия 50 кэВ) через металлическую фольгу (толщиной1 мкм).

Так как дифракционная картина исследовалась для потока электронов, то необ­ходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экс­периментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 10 4 раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электро­нов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдель­ности.

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством нали­чия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рас­считываемой по формуле де Бройля (213.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электронография и нейтронография (см. § 182), а также к возникновению новой отрасли науки — электронной оптики (см. § 169).

Экспериментальное доказательство наличия волновых свойств микрочастиц приве­ло к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и макроскопическим телам. Почему же они не обнаружены экспериментально? Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с = 6,6210 –31 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодомd10 –31 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.

Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы и частотойволн де Бройля:

(213.3)

Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения,справедливого как для фотонов, так и для любых других микрочастиц. Справедливость же соотношения (213.3) вытека­ет из согласия с опытом тех теоретических результатов, которые получены с его помощью в квантовой механике, атомной и ядерной физике.

Подтвержденная экспериментально гипотеза да Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойст­ва; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактовка корпускулярно-волнового дуализ­ма может быть выражена словами академика В. А. Фока (1898—1974): «Можно ска­зать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможностиразличных проявлений свойств, присущих микрообъекту, и состоит дуализм волна—частица. Всякое иное, более буквальное, понимание этого дуализма в вида какой-нибудь модели неправильно.» (в сб.: Философские вопросы современной физики. — М.: Изд-во АН СССР, 1959).

Источник

7. Корпускулярно-волновой дуализм материи. Гипотеза де Бройля, ее экспериментальное подтверждение

Корпускулярно-волновой дуализм — это теория о том, что свет представляется на микроуровне одновременно и как мельчайшие частицы (корпускулы), и как волны. В частности, свет — это и корпускулы (фотоны), и электромагнитные волны.

В 1923 году французский ученый Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия E и импульс p, а с другой стороны — волновые характеристики — частота и длина волны.

В 1948 году это удалось экспериментально подтвердить советскому физику В. А. Фабриканту. Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других, возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов в десятки миллионов раз более интенсивных.

8. Волны де Бройля. Статистический смысл волн де Бройля, свойства волн

Волны де Бройля — волны, связанные с любой микрочастицей и отражающие их квантовую природу. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект — корпускула, но и как волна, причём длина этой волны даётся формулой = h/р, где h = 6.6 . 10 -34 Дж . сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля.

Согласно статистической интерпретации волны де Бройля следует рассматривать как волны вероятности. Более определенно: интенсивность волны де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружить частицу в этом месте.

1) Фазовая скорость волны де Бройля вычисляется в результате дифференцирования этого уравнения по времени: E – p dx/dt = 0,. υ_ф = dx/dt = E/p = mc 2 /mυ = c c/υ, где υ-скорость частицы. Т.к. υc, то фазовая скорость волн де Бройля всегда больше скорости света в вакууме, т.е. υ_ф > c.

Это соотношение отражает особое специфическое свойство волн де Бройля.

2) Групповая скорость волн де Бройля равна скорости движения частиц: υ_r = ds/dt = υ.

3) Длинам боровских орбит соответствуют стоячие волны де Бройля, т.е. в длину боровской орбиты укладывается целое число стоячих волн де Бройля: 2πr_n = nλ.

9. Соотношения неопределенностей Гейзенберга, их физическое содержание

Принцип неопределённости Гейзенберга — в квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы.

Соотношения неопределённости Гейзенберга — это теоретический предел точности любых измерений. Они справедливы для так называемых идеальных измерений, иногда называемых измерениями фон Неймана. Они тем более справедливы для неидеальных измерений или измерений Ландау.

Соответственно, любая частица (в общем смысле, например несущая дискретный электрический заряд) не может быть описана одновременно как «классическая точечная частица» и как волна. (Сам факт того, что какое-либо из этих описаний может быть справедливо, по крайней мере в отдельных случаях, называют корпускулярно-волновым дуализмом). Принцип неопределённости, в виде, первоначально предложенном Гейзенбергом, верен в случае, когда ни одно из этих двух описаний не является полностью и исключительно подходящим, например частица в коробке с определённым значением энергии; то есть для систем, которые не характеризуются ни каким-либо определённым «положением» (какое-либо определённое значение расстояния от потенциальной стенки), ни каким-либо определённым значением импульса (включая его направление).

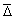
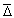
Соотношение неопределенности Гейзенберга показывает, что “между точностью, с которой одновременно может быть установлено положение частицы, и точностью ее импульса существует определенное соотношение”: q p ≥ h ,

где — среднеквадратичное отклонение.

Источник