Трение покоя его природа

Kvant. Трение покоя

Как мы обычно решаем задачи по динамике? Делаем чертеж, изображаем силы и пишем уравнения второго закона Ньютона, проектируя все силы и ускорения на выбранные оси. Чтобы решить полученные уравнения, к ним необходимо добавить формулы, отражающие закономерности, которым подчиняются действующие на тела силы. Например, вместо величины силы тяжести мы подставляем mg (m — масса тела, g — ускорение свободного падэния), вместо силы упругости — kx (k — жесткость, x — величина упругой деформации), силы трения скольжения — μN (μ — коэффициент трения, N — сила нормальной реакции). Еще на стадии составления чертежа мы опираемся на правила для определения направления сил: сила тяжести всегда направлена вниз, сила трения скольжения — против относительной скорости тела и поверхности и т. д.

Однако не все силы имеют свои законы. Так, силу нормальной реакции или силу натяжения нити нам удается определить только благодаря тем ограничениям, которые они накладывают на движение тел. Сила реакции, например, возникает ровно такой величины, чтобы обеспечить движение тела точно вдоль поверхности.

Аналогичными свойствами обладает и известная вам сила трения покоя. Рецепт для определения этой силы выглядит примерно так: сила трения покоя всегда имеет такие величину и направление, чтобы обеспечить покой тела относительно поверхности, по которой оно может двигаться. Эта сила иногда доставляет нам большие неприятности. Первые трудности возникают уже при изображении этой силы на чертеже. Про ее направление известно лишь одно — она направлена по касательной к поверхности. Но в какую сторону? Это не всегда ясно. Кроме того, при решении задач необходимо проверять, что получившееся значение силы трения лежит в допустимых пределах (0 ≤ F_тр ≤ μN); в противном случае начнется проскальзывание. И последнее: сила трения покоя выступает иногда в столь незнакомом обличии (например, в виде силы тяги поезда или машины), что порой бывает трудно ее даже распознать.

Рассмотрим несколько конкретных примеров.

Неподвижное тело

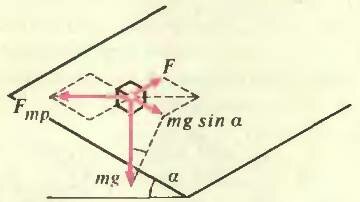
Пусть на тело действуют несколько сил, но при этом оно остается неподвижным. Это означает, что сила трения покоя имеет такие величину и направление, что сумма всех сил равна нулю. Какие же именно?

В простейшем случае (рис. 1) ответ очевиден\[~\vec F_ = -\vec F\]. Если тело лежит на наклонной плоскости с углом α, сила трения направлена вверх вдоль плоскости и равна \(~F_ = mg \sin \alpha\) (m — масса тела). Тело не соскальзывает в том случае, если \(~F_ \le \mu N = \mu mg \cos \alpha\), т. е. если tg α ≤ μ. Теперь приложим к этому телу небольшую горизонтальную силу, направленную вдоль плоскости (рис. 2), и будем увеличивать ее модуль F. При этом \(~\vec F_\) будет изменяться как по величине, так и по направлению. Когда величина силы трения покоя \(~F_ = \sqrt<(mg \sin \alpha)^2 + F^2>\) достигнет значения \(~\mu N = \mu mg \cos \alpha\), начнется проскальзывание тела, причем в сторону, противоположную направлению \(~\vec F_\) в этот момент.

Тело на движущейся тележке

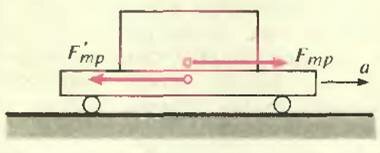
Пусть тележка разгоняется по горизонтальной плоскости с ускорением \(~\vec a\) (рис. 3). Чтобы тело массой m, находящееся на тележке, двигалось вместе с ней, сила трения покоя должна придать телу такое же ускорение \(~\vec a\), как у тележки. Таким образом, \(~\vec F_\) направлена вперед и равна \(~F_ = ma\). Проскальзывания не будет в том случае, если \(~F_ \le \mu N = \mu mg\); если же ускорение тележки превысит величину \(~a_0 = \mu g\), тело с нее соскользнет назад. На рисунке 3 изображена также сила трения \(~\vec F\ ‘_\), действующая на тележку со стороны тела по третьему закону Ньютона \(~\vec F\ ‘_ = -\vec F_\).

Тело на вращающейся платформе

Ускорение тела, неподвижного относительно вращающейся платформы, должно быть направлено к центру платформы. Так как сила трения — единственная горизонтальная сила, которая может сообщить это ускорение, она направлена к центру и равна \(~m \omega^2 r\) (рис. 4, а). Если очень медленно увеличивать угловую скорость вращения платформы ω, то в тот момент, когда сила трения покоя достигнет величины \(~\mu N = \mu mg\), тело начнет соскальзывать с платформы. Если же платформа раскручивается быстро, то кроме центростремительного (или так называемого нормального) ускорения нужно учитывать еще одно ускорение, направленное вдоль скорости и отвечающее за изменение модуля скорости (так называемое тангенциальное ускорение, в случае медленного раскручивания мы им пренебрегли). Это значит, что сила трения покоя, обеспечивающая оба эти ускорения, точнее — две составляющие ускорения (оно, конечно же, всегда одно), будет направлена не строго в сторону центра, а под некоторым углом к радиусу (рис. 4, б).

Колесо на наклонной плоскости

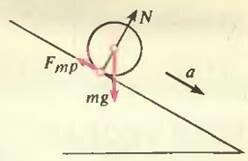
Пусть колесо скатывается с наклонной плоскости, но проскальзывание между колесом и плоскостью отсутствует. Это означает, что те точки колеса, которые в данный момент соприкасаются с плоскостью, являются в этот момент неподвижными. При этом сила трения покоя имеет такую величину, чтобы обеспечивать «раскручивание» колеса (рис. 5). Если бы сила трения отсутствовала, то имело бы место не скатывание колеса, а его соскальзывание — колесо двигалось бы вдоль плоскости поступательно, без вращения.

Разгон покоящегося автомобиля

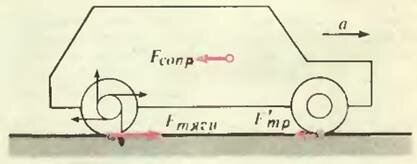
Заметим, что сила тяги мотора, разгоняющая машину, есть не что иное, как действующая на ведущие (задние) колеса сила трения покоя. На вал машины со стороны мотора через передачу действуют силы, которые пытаются повернуть колеса по часовой стрелке (рис. 6). Препятствуя проскальзыванию, и возникает сила трения покоя, направленная вперед и приводящая в движение автомобиль.

А как насчет ведомых (передних) колес — действует ли на них сила трения покоя? Да, действует, но гораздо меньшей величины, а именно такой, которая необходима для раскручивания этих колес.

Кроме этих сил, в горизонтальном направлении действует еще сила сопротивления движению, которая состоит из двух частей: силы трения качения, связанной с деформацией поверхности колеса и с неровностями на дороге, и силы сопротивления воздуха.

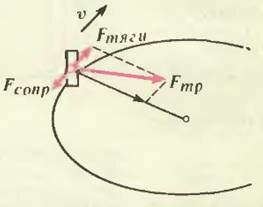
Машина на повороте

Пусть автомобиль совершает поворот, двигаясь с постоянной по величине скоростью. Тогда ускорение машины направлено к центру закругления, перпендикулярно скорости машины.

В эту же сторону направлена и сила трения покоя, действующая на колеса, которые катятся без проскальзывания. К сожалению, школьники часто принимают эту силу трения за силу трения скольжения (ведь автомобиль движется!) и направляют ее против скорости. Но тогда сразу возникает вопрос: а какая же сила создает центростремительное ускорение?

Интересно, что, кроме силы трения покоя, на машину и в самом деле действует сила сопротивления движению, направленная против скорости. Влияет ли она на силу трения покоя? В принципе влияет. Так как машина движется с постоянной скоростью, то сила сопротивления должна быть скомпенсирована такой же по величине силой тяги, т. е. дополнительной силой трения покоя, направленной вперед по ходу движения. Это значит, что результирующая сила трения покоя направлена под углом к радиусу (рис. 7): одна ее составляющая создает центростремительное ускорение, а другая — компенсирует силу сопротивления. На плохой дороге сила сопротивления может быть немалой, и этим обстоятельством пренебрегать нельзя. Ведь проскальзывание (и потеря управления!) произойдет в тот момент, когда именно эта полная сила трения покоя достигнет величины \(~\mu N = \mu mg\). Правда, в теоретических задачах обычно молчаливо подразумевается, что силой сопротивления можно пренебречь. Ну, а в жизни?!

Источник

Силы трения: природа сил трения; коэффициент трения скольжения; закон сухого трения; трение покоя; учет и использование трения в быту и технике.

Равновесие твердых тел: момент силы; условия равновесия твердого тела; устойчивость тел; виды равновесия; принцип минимума потенциальной энергии.

• Моментом силы называется произведение модуля силы на плечо. Плечом называется кратчайшее расстояние от оси вращения до линии действия силы. Модуль момента силы равен
• Абсолютно твердое тело (деформация пренебрежимо мала) находится в равновесии (состояние покоя или равномерного и прямолинейного движения), если сумма действующих на него внешних сил равна нулю. Кроме того, сумма моментов внешних сил равна нулю.
• Устойчивость тела зависит от положения центра тяжести и от величины площади опоры: чем ниже центр тяжести и больше площадь опоры, тем тело устойчивее.
• Виды равновесия: устойчивое (после воздействия силы тело вернется в первоначальное положение), неустойчивое (после воздействия силы, тело не возвратится на прежнее положение), безразличное (равнодействующая сила = 0)
• Принцип минимума потенциальной энергии: Любая замкнутая система стремиться перейти в такое состояние, в котором ее потенциальная энергия минимальна.

1. Механическая работа. Мощность. Энергия: кинетическая энергия; потенциальная энергия тела в однородном поле тяготения и энергия упруго деформированного тела; закон сохранения энергии;закон сохранения энергии в механических процессах; границы применимости закона сохранения механической энергии;работа как мера изменения механической энергии тела.

• Работ силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними ( ). Работа силы тяжести равна разности потенциальных энергий ( ). Работа силы тяжести по наклонной плоскости равна разности кинетических энергий ( ). Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела ( ).
• Мощностью называют отношение работы к интервалу времени, за который эта работа совершена .
• ЗСЭ. Механическая энергия не возникает из ничего и не может исчезнуть никуда.

Источник