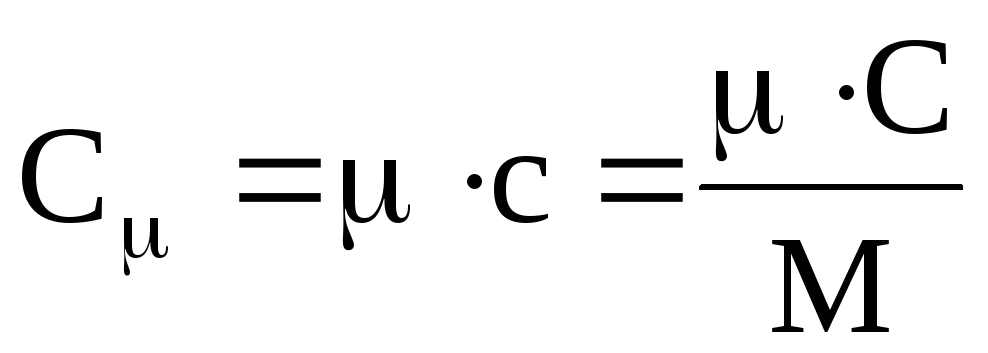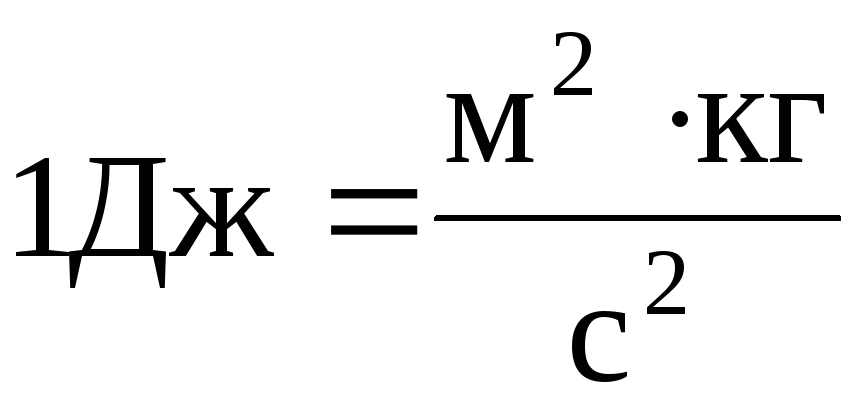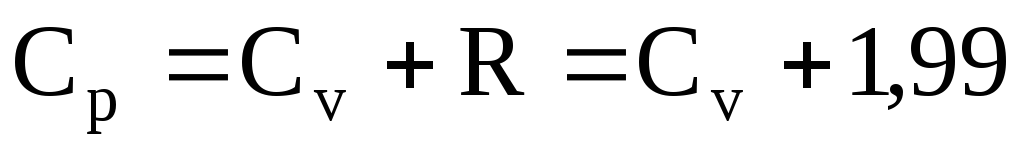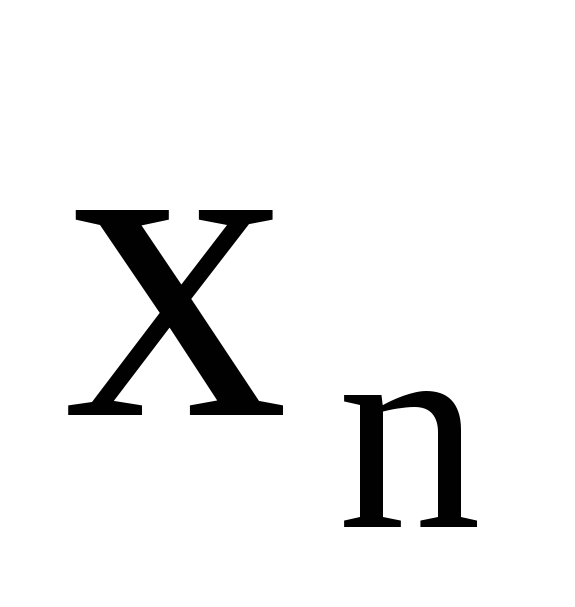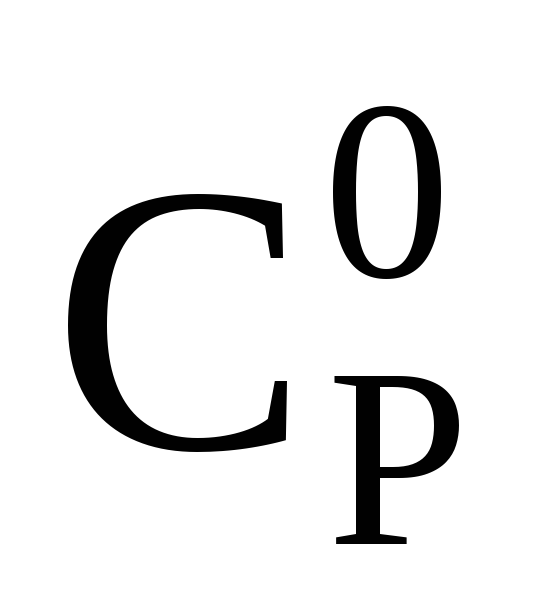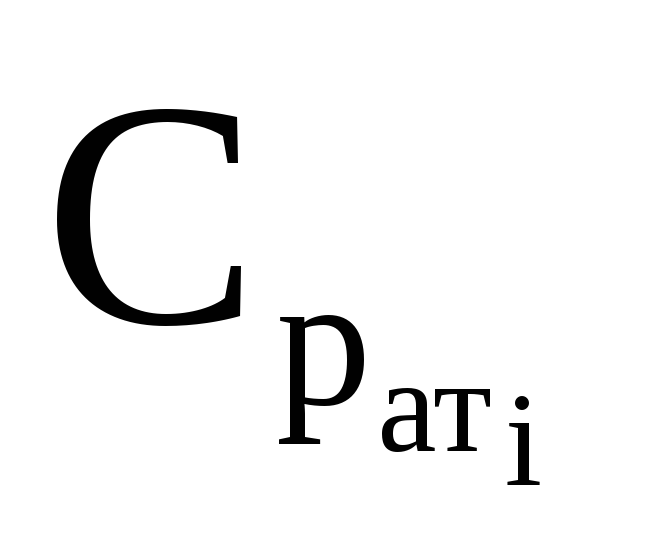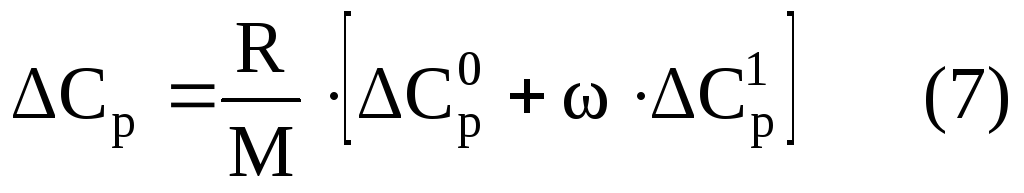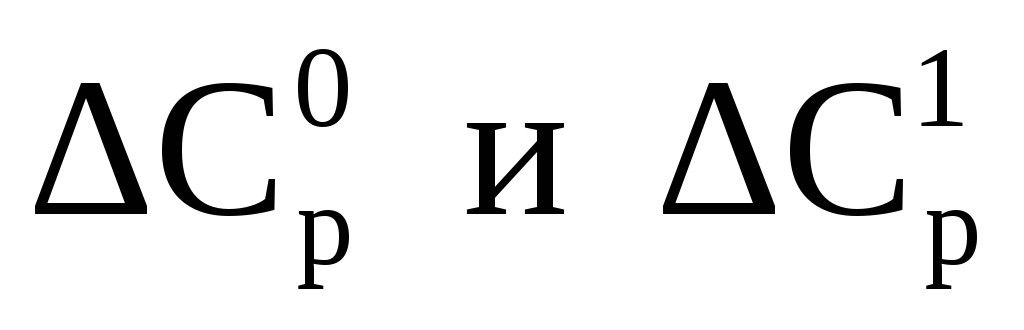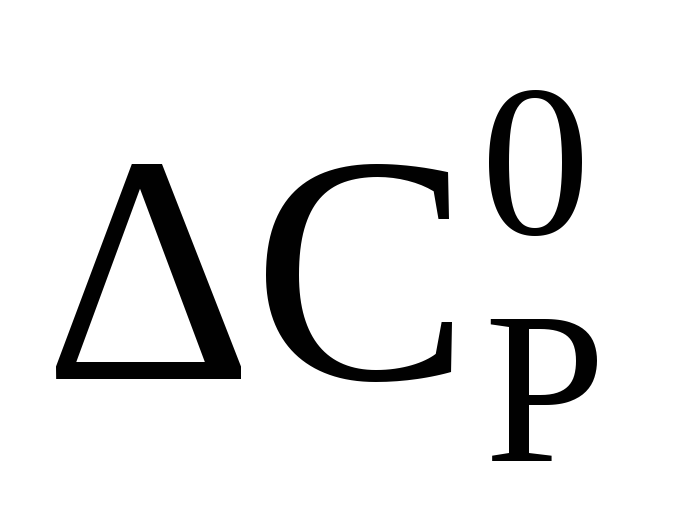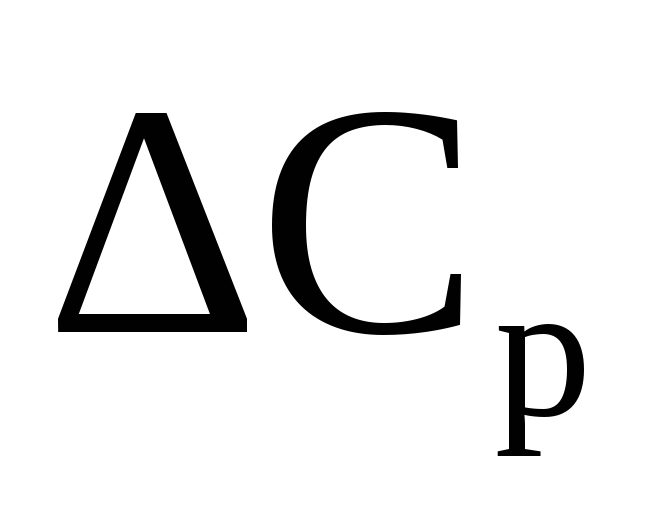Удельная теплоемкость природных газов

§ 9. Определение изобарной молярной теплоемкости природных газов

где индексы у скобок означают давление р = const и объем V= const.

Согласно первому началу термодинамики имеем dQ=dt—Vdp, (III. 60)

где Q — количество теплоты; V — объем системы; i— энтальпия (теплосодержание). di = c_pdT + . (III.61)

При изобарном процессе (р = const) изменение количества теплоты системы равно изменению ее энтальпии dQ = di = C_pиdT (II1.62)

Изобарная молярная теплоемкость идеальных газов Сри за­висит от температуры. Зависимость молярной теплоемкости компонентов природных газов при атмосферном давлении от температуры приближенно можно выразить формулой

С_ри = 0,523 (8,36+0,00892t) , кДж/(кмоль-К), (III.64)

где Mi — молекулярная масса углеводорода, являющегося ком­понентом природного газа (от метана до гептана включительно)

Погрешность расчетов по формуле (III. 64) для углеводоро­дов CH₄-C₅H₁₂ в интервале температур минус 40 °С плюс 120 О С не превышает 5%, для углеводородов С₆Н₁₄—С₇Н₁₆ в том же интервале температур не превышает 10 %.

Изобарная молярная теплоемкость неуглеводородных ком­понентов природных газов (азота, углекислого газа, сероводо­рода) равна примерно половине теплоемкости углеводорода с одинаковой молекулярной массой при одинаковой темпера­туре.

Например, изобарная молярная теплоемкость CO₂(C_ри=44) равна половине молярной теплоемкости пропана С₃Н₈ (С_ри=44), которая рассчитывается по формуле (111.64).

Теплоемкость смесей газов определяется по правилу адди­тивности(II1.65)

где y_i — молярная доля i-ro компонента в смеси; c_pi — изобар­ная молярная теплоемкость i-ro компонента.

Изобарная молярная теплоемкость реальных природных га­зов зависит от давления и температуры С_р = С_ри(t) + С_р(р, t), (Ш.66)

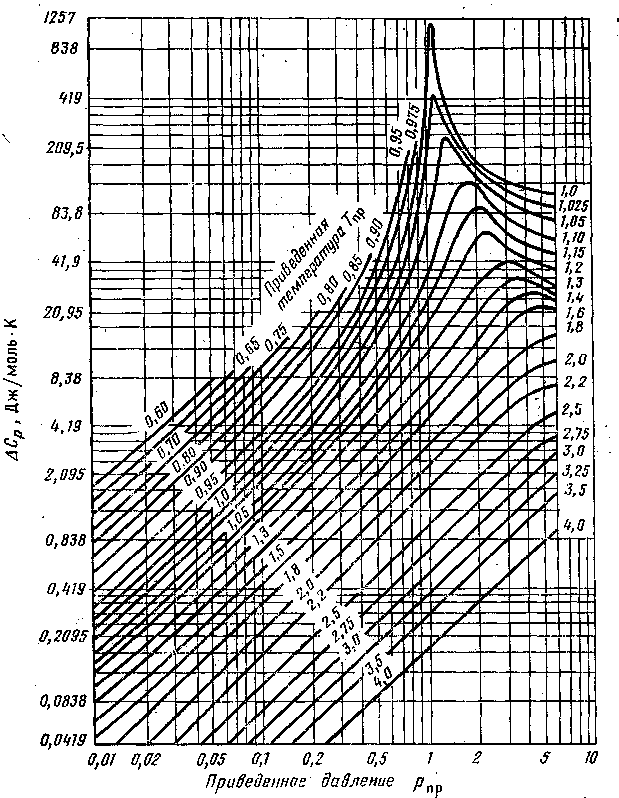
где С_р(р, t) —изотермическая поправка теплоемкости на дав­ление (рис. III.9).

Изобарную молярную теплоемкость природного газа можно рассчитать и по формуле, предложенной Л. М. Гухманом и Т. В. Нагаревой:

При решении задач, связанных с добычей, транспортом, хранением и переработкой природных газов, наиболее употре­бительны двухконстантные уравнения состояния и восьмиконстантные.

Р ис. III.9. Зависимость изотермической поправки изобарной мольной теплоемкости С_р(р, t) от приведенных абсолютных давления р_пр и температуры Т_пр

Последней, наиболее удачной модификацией двухконстантного уравнения состояния природных газов, предложенной в 1975 г., является уравнение состояния Пенга — Робинсона

где V —молярный объем; а(Т), b — коэффициенты уравнения, определяемые критическими параметрами вещества (коэффи­циент а(Т) —фракция температуры).

Уравнение состояния Пенга—Робинсона, записанное отно­сительно коэффициента сверхсжимаемости z, имеет вид z 3 -(1-В)z 2 +(А-3В 2 -2В)z-(АВ—В 2 -B 3 )=0, (69)

Уравнение (III.69) имеет один или три действительных корня. Если смесь находится в двухфазном состоянии, то больший корень относится к паровой фазе, а наименьший положитель­ный корень — к жидкой фазе.

При критических условиях (z_кp = 0,307)

При температурах, отличных от критической,

где — безразмерная функция приведенной темпера­туры Т_пр и ацентрического фактора ; при критической темпе­ратуре =1.

Для всех веществ зависимость между  0,5 и Т 0,5 _пр может быть аппроксимирована уравнением прямой  0,5 =1+m(1- Т 0,5 _пр), (III.73)

где коэффициент m, определяющий угол наклона прямой к оси Т 0,5 _пр, является функцией ацентрического фактора : m=0,37464+1,5422b—0,26992 2 . (III.74)

При использовании уравнения Пенга—Робинсона для расчета термодинамических и физических свойств многокомпонентных смесей коэффициенты а_cм(Т) и b_см вычисляют по следующим формулам:

Отклонение теплофизических свойств реальных природных га­зов от идеальных можно определить с использованием уравне­ния состояния Пенга — Робинсона.

Отклонение энтальпии реального газа

г де Н° — энтальпия идеального газа.

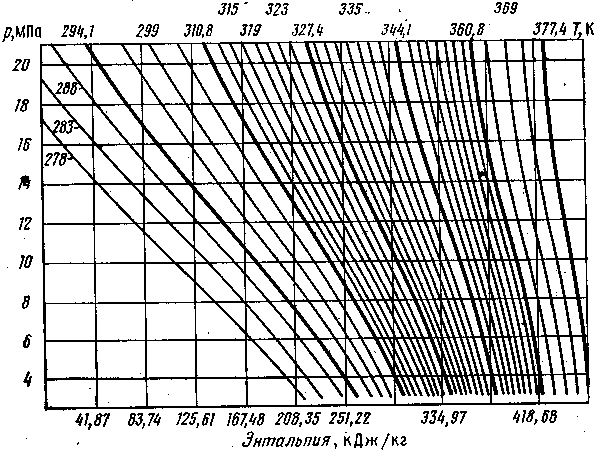
Энтальпийная диаграмма природного газа изображена на рис. III.10.

Рис. III.10. Энтальпийная диаграмма природного газа

Отклонение молярной изобарной теплоемкости реального газа

Зависимость С_р от р_пр и Т_пр изображена на рис. III.9

Разность изобарной и изохронной молярных теплоемкостей реального газа

Источник

Термодинамические характеристики газа

В технологических расчётах добычи и транспорта газа часто пользуются основными термодинамическими характеристиками природного газа: теплоемкостью, энтропией, энтальпией, теплотой сгорания, теплообменом, теплопроводностью.

Теплоёмкость. Теплоёмкостью называют количество теплоты, необходимое для нагревания единицы массы или объёма вещества на 1° С.

Отношение теплоёмкости в массе системы М называется удельной теплоёмкостью: с = С/М, а отношение теплоемкости к количеству вещества – молярной теплоёмкостью:

. (1)

Единицей количества теплоты, работы, энергии в системе СИ является джоуль (Дж). Джоуль — работа силы 1 Н при перемещении ею тела на расстоянии 1 м в направлении действия силы:

Теплоёмкость выражается в Дж/К, удельная теплоёмкость – в Дж/(кг·K), молярная теплоёмкость – в Дж/(моль К).

Теплоёмкость природных газов зависит от химического состава и состояния, а также от процесса сообщения им теплоты. В адиабатическом процессе С = 0, в изобарическом С = Ср, в изохорическом С = Сv.

Для газов обычно различают теплоёмкости при постоянном объёме Сv и постоянном давлении Ср.

(2)

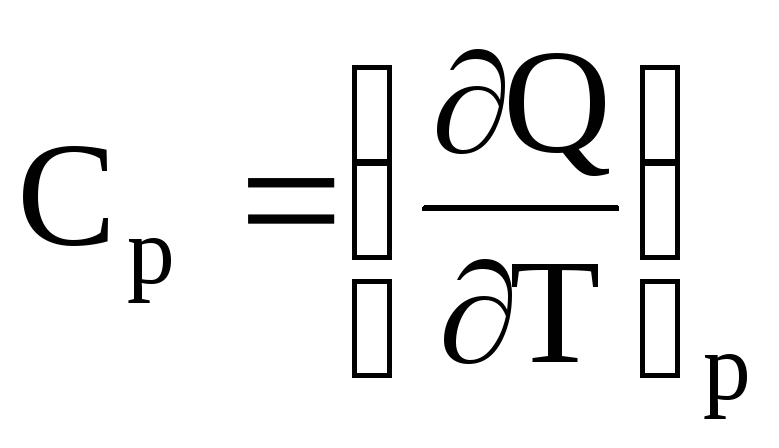
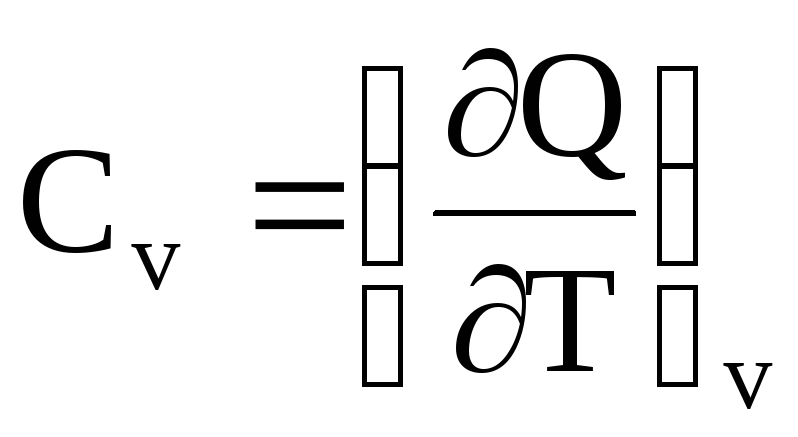
Теплоёмкости при постоянном объёме Сv связана с процессом, характеризующимся тем, что при неизменности объёма вся энергия, сообщаемая газу в форме теплоты, затрачивается на увеличение внутренней энергии газа. С_рсвязана с процессом, характеризующимся тем, что, нагревая тело, предоставляют ему возможность расширяться при неизменном давлении. Таким образом, часть сообщенной телу теплоты идет на производство работы расширения. ПоэтомуС_р > С_v.

Для идеальных газов между С_риС_v существует следующее соотношение в [кал/моль·°С]:

(3)

где R— газовая постоянная.

В области давлений, где газы считаются идеальными, значения теплоёмкостей постоянны. Однако для реальных газов значения теплоёмкости изменяются в зависимости от давления и температуры.

Для смеси газов теплоёмкость определяется по сумме теплоемкости входящих компонентов по формуле

(4)

где С₁, С_2…С_n— теплоёмкости отдельных компонентов смеси;

х₁, х₂…содержание компонентов в долях единицы.

Отношение теплоёмкости называют показателем адиабаты.

Для практических целей с достаточной точностью можно использовать формулу следующего вида:

где С_р– изобарная теплоёмкость;

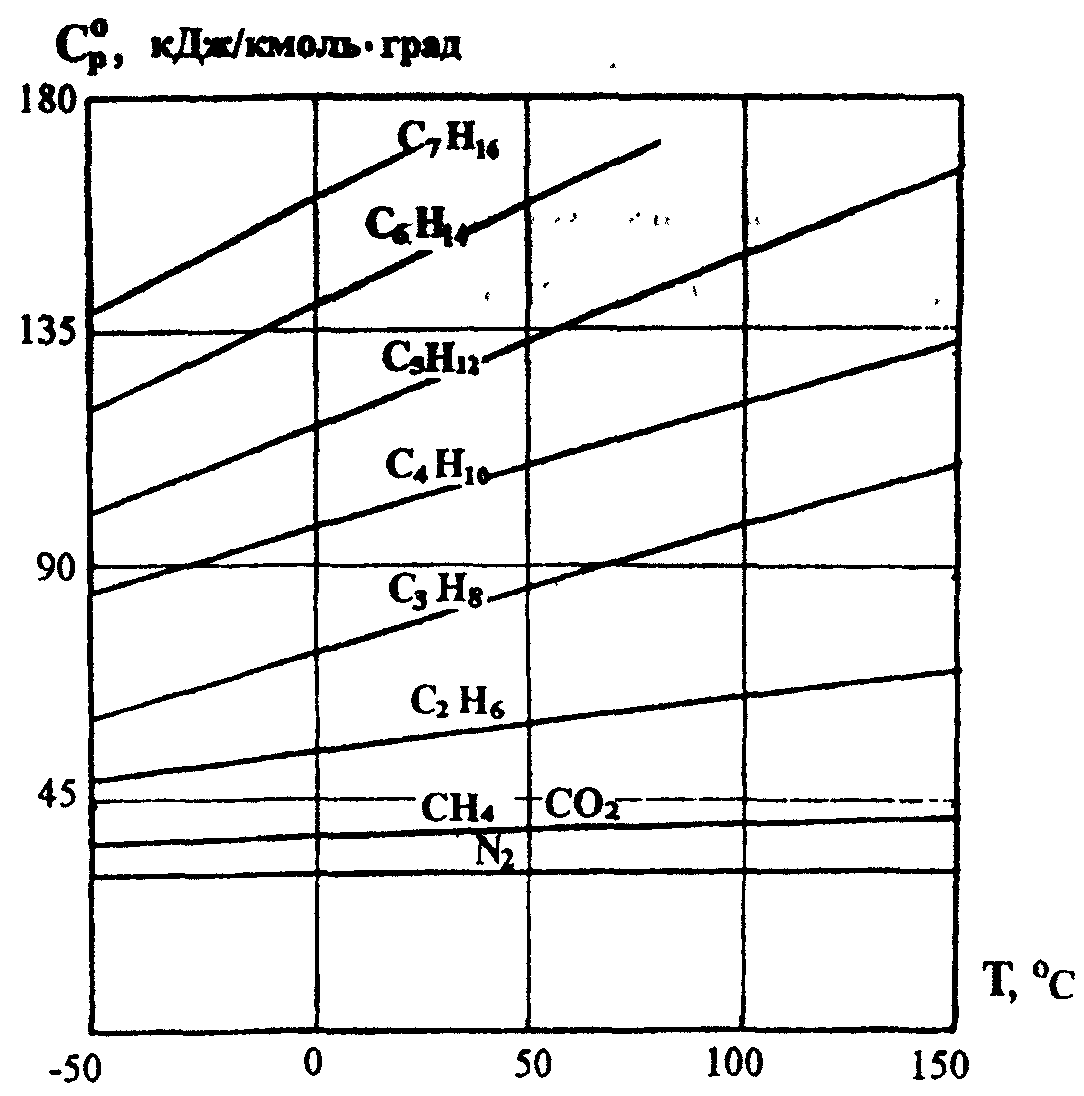
С_{р ат}– теплоёмкость при атмосферном давлении и заданной температуре, определяемая из рисунка 1 и расчётным путём.

Рисунок 1. Зависимость изобарной молярной теплоёмкости природных газов от температуры при давлении Р = 0,1 МПа

Аналитически С_{р ат}определяется по формуле следующего вида

где Е_i, F_i, H_i, N_i– коэффициенты, определяемые из таблицы 1;

Т – температура, при которой определяется .

Изотермическая поправка на давление ΔС_рможет быть определена как графическим путем, так и расчётным, например, по формуле следующего вида

где R – газовая постоянная, равная R = 1,986 ккал/моль;

М – молекулярная масса газа;

— поправки на теплоёмкость, зависящие от приведенных давления и температуры, определяемые по зависимостям, приведенным на рисунках 2 и 3.

Рисунок 2. Зависимость поправочной от приведенных давления и температуры

Величина может быть определена и без учёта фактора ацентричности ω по графической зависимости приведенной на рисунке 4.

Рисунок 3. Зависимость поправочной величины т приведенных давления и температуры

Фактор ацентричности молекул газа ω определяется аналогично, как и при определении коэффициента сверхсжимаемости Z.

Величину С_р(Р, Т) можно рассчитать по формуле вида

(8)

где Т — температура газа, 0 С;

М – молекулярная масса газа.

Таблица 1. Значения коэффициентов для зависимости (6)

Источник