Лекция 1 Квантовая природа электромагнитного излучения
Классические представления о волновой природе электромагнитного излучения позволили успешно объяснить явления интерференции, дифракции и поляризации и создать высокоточную теорию оптических приборов. Однако исследование процессов взаимодействия электромагнитных волн с веществом выявило ограниченность области применимости этих представлений. С точки зрения классической теории ускоренно движущийся заряд излучает или поглощает электромагнитные волны, интенсивность которых пропорциональна квадрату ускорения. Для непериодического движения интенсивность волны отлична от нуля в широком интервале частот. Такой спектр излучения называется сплошным. Если движение частицы является гармоническим с частотой , то излучаемая волна имеет ту же частоту. Спектр излучения, содержащий дискретный набор частот, называется линейчатым или дискретными.
Проблема устойчивости атомов. Опытами Резерфорда было установлено, что в целом нейтральный атом состоит из малого в сравнении с ним положительного ядра, в котором сосредоточена почти вся масса (>99%), и электронов. Согласно теореме Ирншоу (см. лекцию № 3 в [3]) эта система не может быть устойчивой, находясь в покое. Поэтому Резерфорд пришел к так называемой планетарной модели атома, в которой электроны вращаются вокруг ядра подобно планетам солнечной системы. По законам классической электродинамики такие электроны должны непрерывно излучать, поскольку под действием притяжения ядра испытывают ускорение. В результате электроны должны быстро (за время ~10 -11 с) упасть на ядро. Таким образом, и при наличии движения в рамках классической физики модель взаимодействующих по закону Кулона зарядов оказывается неустойчивой.
Устойчивость классическому атому могут придать некулоновские силы. Но и они не спасают положение. В этом случае не удается объяснить атомные спектры. При любых силах спектр классического излучения должен либо быть непрерывным, либо состоять из основных частот и кратных им гармоник. На самом деле кратных частот в дискретных спектрах атомов не наблюдается. Таким образом, устойчивость атомов и характер их спектров не могут быть объяснены в рамках классической физики.
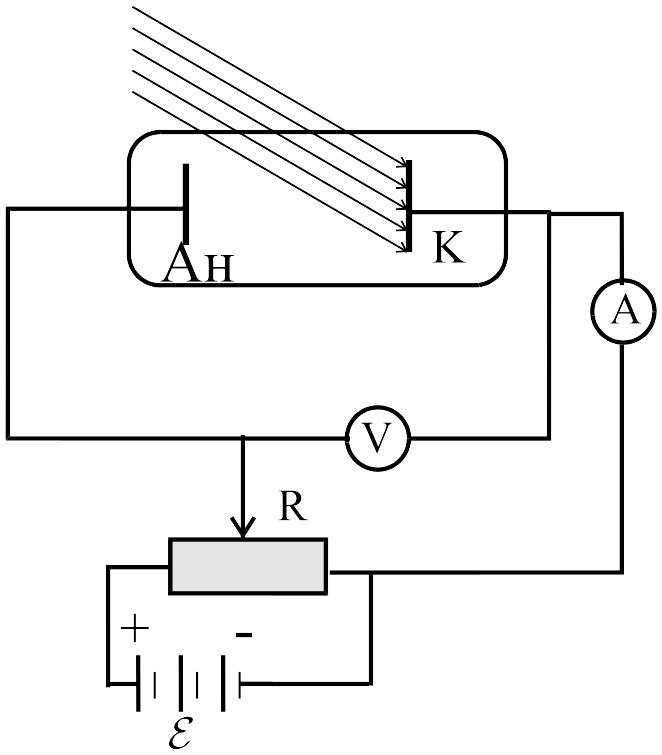
Фотоэффект. Явное несоответствие выводов, следующих из классической теории, экспериментальным данным обнаружилось при изучении фотоэффекта. Вырывание электронов с поверхности металлов под действием электромагнитной волны называется внешним фотоэффектом. При внутреннем фотоэффекте в объеме вещества увеличивается концентрация свободных электронов, в результате чего увеличивается его электропроводность. Схема установки по исследованию внешнего фотоэффекта (в дальнейшем — фотоэффекта) приведена на рис. 1.1. Катод К облучается электромагнитными волнами видимого или ультрафиолетового диапазона. Амперметр А измеряет ток, протекающий между катодом и анодом Ан (фототок). Батарея источников Э.Д.С. и переменное сопротивление R позволяют изменять как величину, так и знак напряжения U между катодом и анодом, измеряемого вольтметром V. Изменяя подключение батареи, можно изменять также и знак напряжения.
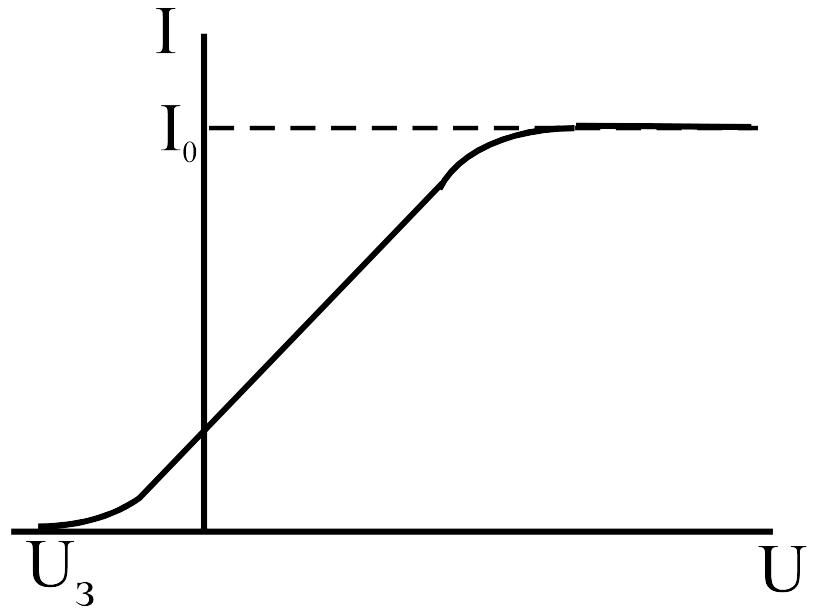
В ольт-амперная характеристика фотоэффекта приведена на рис. 1.2. Здесь положительным считается напряжение, при котором катод заряжен отрицательно. С ростом U фототок растет и достигает своего максимального значения IН, называемого током насыщения в том случае, если все выбитые с катода заряды достигают анода. Знак U свидетельствует о том, что поверхность катода покидают отрицательные заряды – электроны. Модуль отрицательного напряжения UЗ, при котором фототок прекращается, называется задерживающим напряжением.
Величина UЗ позволяет определить энергию eUЗ, которой обладает фотоэлектрон. Систематические исследования, выполненные профессором Московского университета А.Г. Столетовым, позволили сформулировать следующие законы фотоэффекта:
- Фототок пропорционален интенсивности излучения.
- Существует длина волны КР (красная или более точно длинноволноваяграница фотоэффекта), разграничивающая области излучения, способного (КР) и неспособного (>КР) вызывать фотоэффект. Величина КР зависит от материала катода и не зависит от интенсивности излучения.
- Энергия фотоэлектрона E линейно зависит от частоты волны и не зависит от интенсивности излучения.
- Фототок возникает практически мгновенно после начала облучения катода. На этом свойстве — безынерционости фотоэффекта — основаны многие его практические применения.
По классическим представлениям энергия волны, а следовательно, и энергия, поглощаемая частицей, пропорциональна интенсивности падающего излучения. Поэтому с классической точки зрения наличие красной границы при любой интенсивности и независимость энергии фотоэлектрона от интенсивности не могут быть объяснены. Время накопление энергии частицей в классической физике определяется мощностью источника. В стандартных условиях эксперимента электрон может поглотить непрерывно распространяющуюся энергию, достаточную для отрыва от металла, за время, превышающее 1 с, что противоречит безынерционости фотоэффекта.
Фотон. Уравнение Эйнштейна. Для объяснения фотоэффекта Эйнштейн (1905 г.) ввел понятие фотонов, согласно которому излучение переносится квантами (частицами), летящими со скоростью света. Энергия фотонов EФ пропорциональна частоте излучения :
Коэффициент пропорциональности h = 6,62·10 -34 Дж ·с называется постоянной Планка. Согласно специальной теории относительности энергия такой частицы с нулевой массой покоя и движущейся со скоростью света следующим образом связана с ее импульсом:
Следовательно, импульс фотона
Фотон, попадая в металл, отдает свою энергию одному электрону и таким образом выбивает его из металла. При вылете электрон теряет часть энергии A, равную работе, необходимой для его освобождения (работе выхода). Закон сохранения энергии в этом случае имеет вид
Уравнение (1.4), называемое уравнением Эйнштейна, полностью объясняет законы фотоэффекта.
- Число выбитых электронов пропорционально числу падающих квантов, а следовательно, и интенсивности света.
- Если энергия фотона меньше работы выхода, энергия фотоэлектрона остается отрицательной, что объясняет наличие красной границы.
- Из уравнения Эйнштейна непосредственно следует линейная зависимость энергии фотоэлектрона E от частоты волны.
- Квант энергии поглощается электроном практически мгновенно, что объясняет безынерционость фотоэффекта.
Источники интенсивного излучения (лазеры) позволяют наблюдать маловероятные в обычных условиях процессы одновременного поглощения N>1 фотонов – многофотонный фотоэффект. В экспериментах N может достигать значений ~10 2 . Уравнение Эйнштейна в этом случае имеет вид
Эффект Комптона. Явление фотоэффекта доказывает тот факт, что энергетический обмен между светом и веществом носит квантовый характер. Корпускулярная природа света наиболее наглядно проявляется при взаимодействии жесткого рентгеновского излучения с электронами вещества. Поскольку энергия кванта в этом случае много больше работы выхода, электроны можно считать практически свободными.
П оглощение фотона свободным электроном невозможно. В самом деле, запишем законы сохранения энергии и импульса для такого процесса:
откуда получаем запрещенную релятивистской теорией скорость электрона, превышающую скорость света . Поэтому процесс взаимодействия свободного электрона с фотоном имеет характер рассеяния. Это явление наблюдалось Комптоном в 1922 г. Он обнаружил, что длина волны рассеянных рентгеновских лучей вне зависимости от вещества больше, чем у падающих.
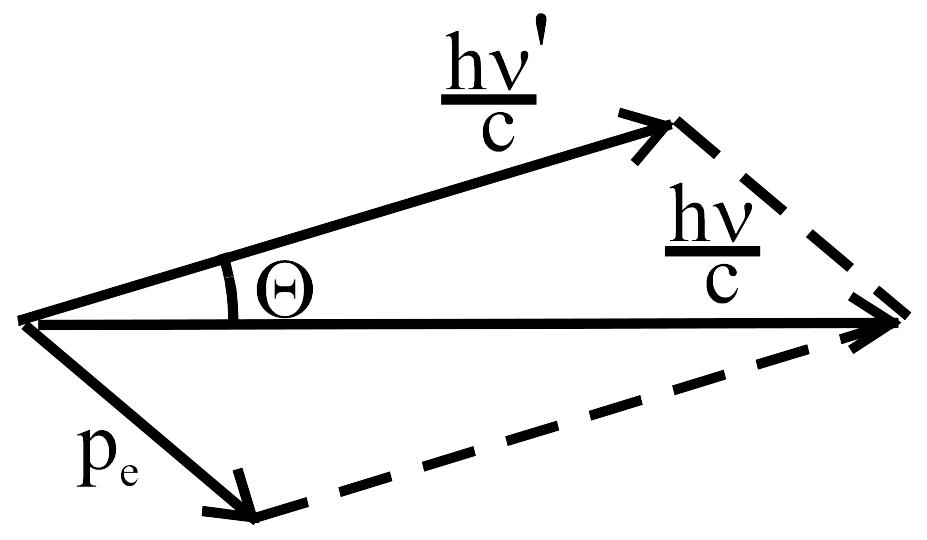
Объяснение наблюдаемого эффекта было получено на основе представлений о неупругом столкновении фотона и электрона (рис. 1.3). В процессе столкновения световой квант с энергией передает ее часть электрону. В результате энергия рассеянного кванта оказывается меньше начальной энергии . Аналогичным образом происходит уменьшение импульса фотона от величины до . Используя законы сохранения полного импульса и полной энергии в релятивистской форме можно получить формулу Комптона для изменения длины волны светового кванта в результате столкновения:
где – угол рассеяния фотона (рис. 1.3), 0= 2,42·10 -12 м – так называемая комптоновская длина волны. Теоретический результат находится в полном согласии с опытом.
Тепловое излучение. В классической физике процесс излучения энергии веществом выглядит следующим образом: колеблющиеся с частотой диполи вещества излучают электромагнитные волны той же частоты. Падающие на пов ерхность тела электромагнитные волны возбуждают вынужденные колебания диполей, что приводит к поглощению энергии. По второму началу термодинамики, замкнутая система стремится к равновесному состоянию.
Излучение, которым обмениваются тела такой системы, называется тепловым или равновесным. Особенно просто выглядят законы теплового излучения для абсолютно черного тела, то есть тела, поглощающего все падающее на него излучение. Именно эти законы и будут рассматриваться в дальнейшем. Тепловое излучение принято описывать в терминах энергетической светимости (в дальнейшем – светимости) R, равной мощности излучаемой единицей поверхности:
и плотности энергетической светимости r, равной энергетической светимости, приходящейся на единичный интервал длин волн
В соответствии с определениями светимость и ее плотность связаны соотношением
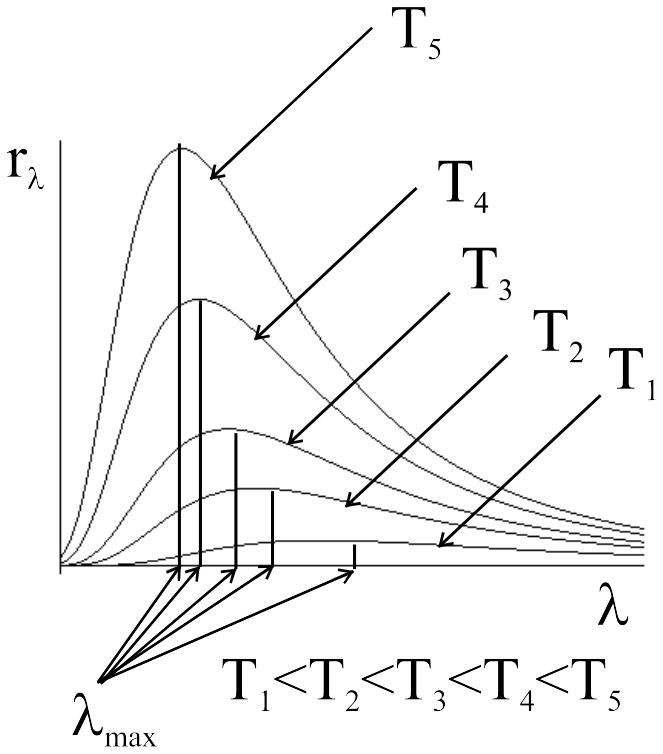
или графическим образом светимости является площадь под кривой r() (рис.1.5).
Экспериментально было установлено, что
- r(0)=r()=0 и длина волны, на которую приходится максимум спектральной плотности, обратно пропорциональна абсолютной температуре:
Этот закон называется законом смещения Вина, а постоянная b —константой Вина.
2.Светимость пропорциональна четвертой степени абсолютной температуры:
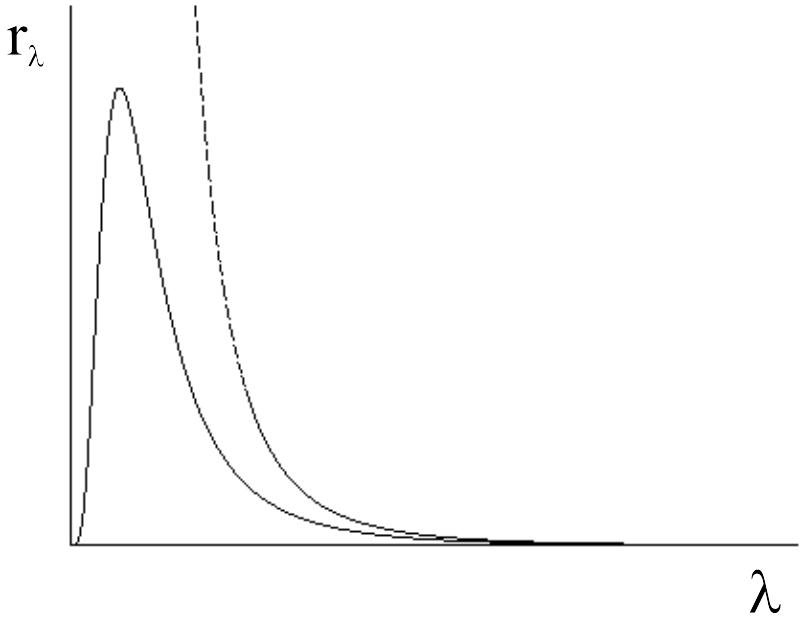
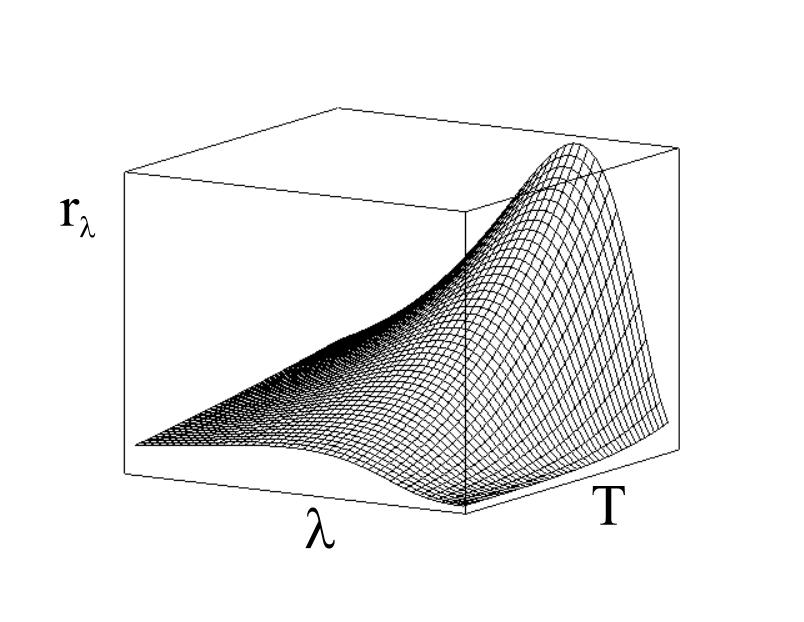
Этот закон называется законом Стефана-Больцмана, а постоянная — постоянной Стефана-Больцмана. Вид экспериментальных кривых r() для фиксированных температур приведен на рис. 1.5. Зависимость r(,Т) отражена на рис. 1.6.
Рис. 1.6
Спонтанное и стимулированное излучение. Расчеты, выполненные в модели классических осцилляторов, привели к абсурдному результату – плотность светимости обратно пропорциональна квадрату длины волны (пунктир на рис. 1.4) и, следовательно, светимость бесконечна. Для того, чтобы описать тепловое излучение, Планку пришлось ввести чуждую классической физике гипотезу, согласно которой излучение и поглощение энергии электромагнитной волны веществом происходит не непрерывно, а квантами, энергия которых определяется формулой (1.2). Рассмотрим, как выглядит процесс излучения и поглощения с квантовой точки зрения. Частицы вещества могут находиться только в определенных дискретных стационарных состояниях с энергиями , , ,… Состояние с наименьшей энергией является устойчивым и называется основным состоянием. Частица может поглощать лишь излучение с такой частотой, что энергия фотонов равна энергии, необходимой для перехода из одного стационарного состояния с энергией в другое стационарное состояние с энергией ( ) так, что
Возможен также и обратный процесс перехода атома из возбужденного состояния в состояние с меньшей энергией, сопровождающийся излучением фотона. Излучение может происходить как самопроизвольно (спонтанно), так и вынужденно, под действием уже имеющихся фотонов с частотой , соответствующей атомному переходу. Вынужденное излучение называют также индуцированным или стимулированным. Вероятность спонтанного излучения в единицу времени не зависит от внешних условий и для данного перехода является некоторой константой . Вероятность индуцированного излучения, так же как и вероятность поглощения фотонов, пропорциональна энергетической плотности фотонов . Эти вероятности равны и , где и – соответствующие коэффициенты. Вероятности индуцированных прямых и обратных переходов равны и, следовательно,
Формула Планка. В тепловом равновесии доля атомов в состоянии m выражается через долю атомов в состоянии n согласно распределению Больцмана:
С другой стороны, в равновесии процессы поглощения и излучения идут с одинаковой интенсивностью, то есть
С учетом формулы (1.15) получим
Подставляя уравнение (1.14) в (1.17), имеем
Из квантовой теории излучения можно определить и величину
Источник