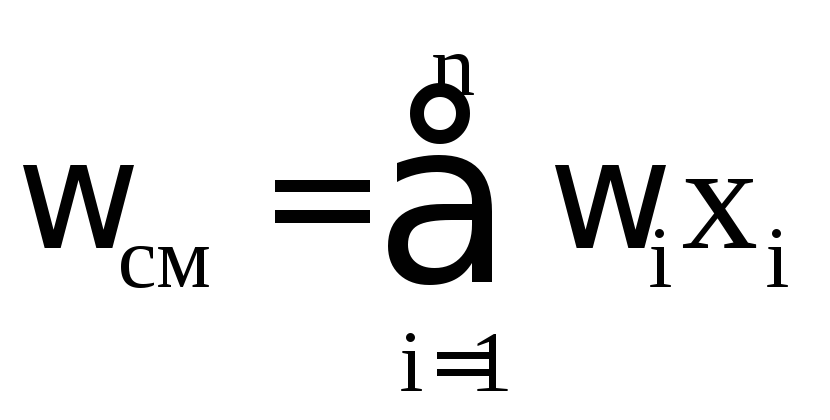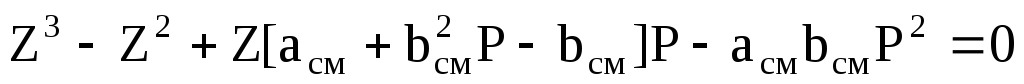2.2.5 Коэффициенты сверхсжимаемости газов (рис стр-44-56)
Коэффициент сверхсжимаемости газов – это отношение объема υ при заданных значениях Р и Т к объему этого газа, определенному при идентичных Р и Т по законам идеального газа υид. Коэффициент сверхсжимаемости характеризует отклонение объема реального газа от объема “идеального”. Формула, связывающая основные параметры газа – объем, давление и температуру, называется уравнением состояния газа. Уравнение состояния идеального газа получено из условия отсутствия межмолекулярных взаимодействий и без учета объема самих молекул и имеет вид
где n – число молей газа; R – универсальная газовая постоянная; Т и Р – температура и давление газа.
Уравнение состояния реального газа может быть представлено в виде:
Универсальная газовая постоянная R выражает работу одного моля газа при повышении его температуры на один градус и в системе СИ имеет размерность Дж/кмоль·град.
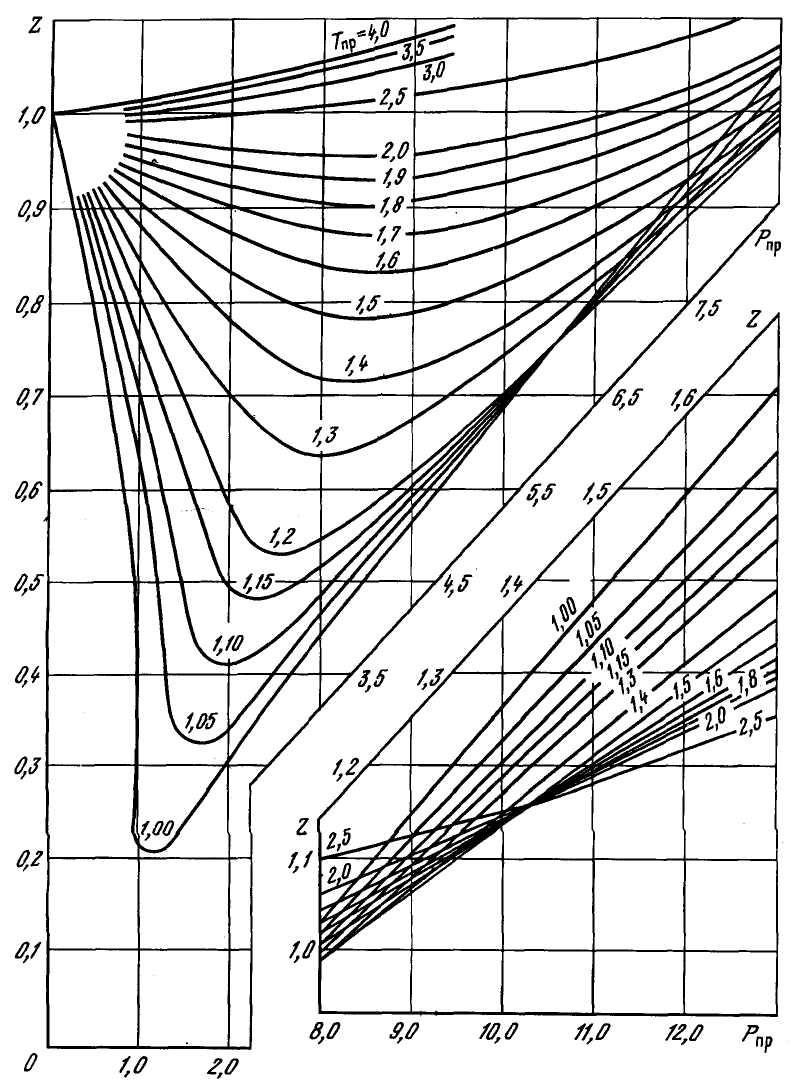
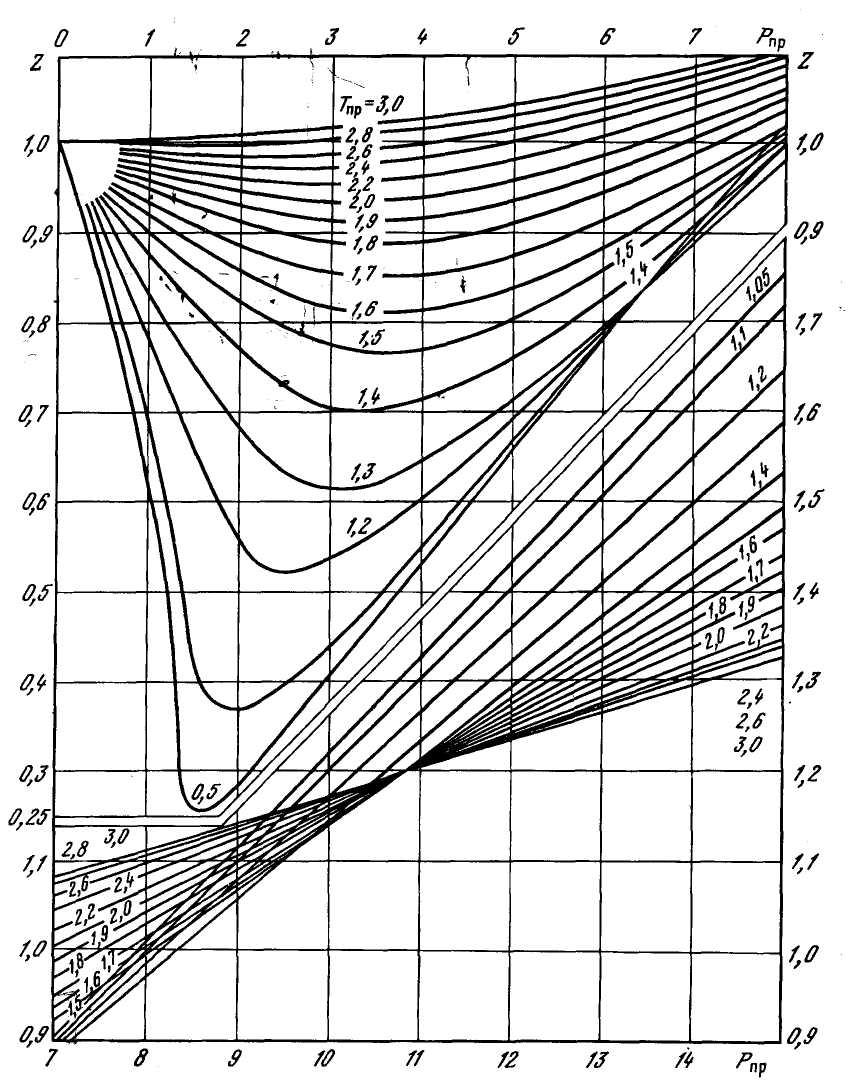
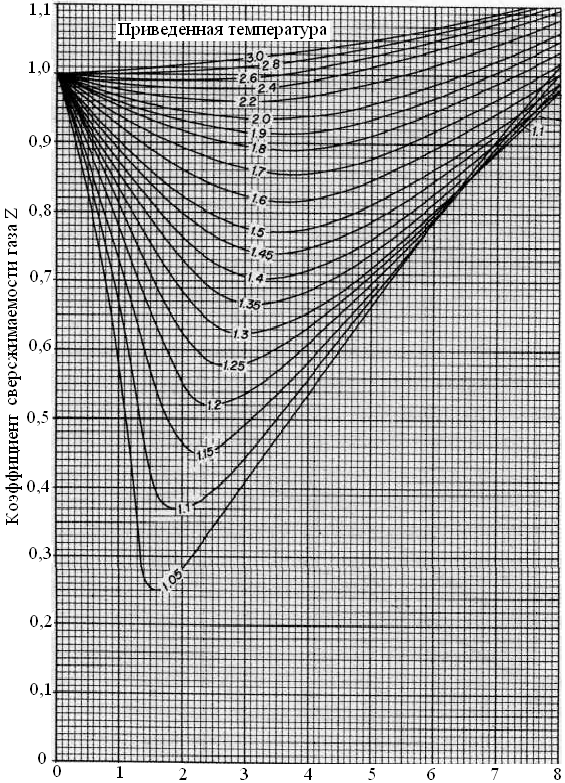
Коэффициент сверхсжимаемости газа Z зависит от состава газа, давления и температуры. Значение коэффициента может быть определено графическим и аналитическим способами. Способ определения следует выбирать, исходя из требуемой точности его значения. Наиболее простым способом определения Z является графический. Для определения Z природных газов, содержащих не более 2% (мольных) высококипящих углеводородов С5+, 2% ароматических углеводородов и около 5% полярных и кислых компонентов, можно использовать графическую зависимость Z от приведенного давления Рпр и приведенной температуры Тпр, показанных на рисунках 2.4 и 2.5. На рисунках 2.6÷2.8 приведены зависимости Z от Р и Т для N2, CO2 и H2S.
При более высоком содержании в газе высококипящих углеводородов С5+ и полярных компонентов коэффициент сверхсжимаемости Z следует определять с учетом ацентричного фактора по формуле:
где Z (0) , Z (1) – коэффициенты, определяемые из графиков зависимостей Z (0) и Z (1) от приведенных параметров Рпр и Тпр, показанных на рисунках 2.9 и 2.10; ωсм – фактор ацентричности, определяемый по известному составу газа по формуле:
(2.22)
где ωi – фактор ацентричности i-го компонента, определяемый из таблицы 2.2 или по формуле (2.6).
Псевдокритические параметры, необходимые для определения Рпр и Тпр, с помощью которых из графиков находят Z (0) и Z (1) , должны быть определены в зависимости от состава газа. Если в газе количество высококипящих углеводородов и полярных веществ более 5%, то псевдокритические параметры должны быть определены согласно [18]:
Рисунок 2.4 – Зависимость коэффициента сверхсжимаемости Z метана от приведенных давления и температуры.
Рисунок 2.5 – Зависимость коэффициента сверхсжимаемости Z природного газа от приведенных давления и температуры.
Рисунок 2.6 – Зависимость коэффициента сверхсжимаемости Z азота от давления и температуры.
Рисунок 2.7 – Зависимость коэффициента сверхсжимаемости Z углекислого газа от давления и температуры.
Рисунок 2.8 – Зависимость коэффициента сверхсжимаемости Z сероводорода от давления и температуры.
Рисунок 2.9 – Зависимость коэффициента сверхсжимаемости Z (0) простых веществ от приведенных давления и температуры.
Рисунок 2.10 – Зависимость коэффициента сверхсжимаемости Z (1) несферических молекул от приведенного давления и температуры.
Если в газе содержится более 5% СО2, то значение Z должно быть рассчитано следующим образом:
– по формулам (2.3) вычисляют псевдокритические давление Рпк и температуру Тпк;
– вычисляется фактор ацентричности смеси ωсм, исключая из нее СО2, по формуле:
(2.23)
– по известной величине ωугл и концентрации СО2 в газе из графика, показанного на рисунке 2.11а и б, определяется величина ε, являющейся температурной поправкой для используемой при расчетах псевдокритической температуры. При наличии в газе СО2 и H2S значение ε может быть рассчитано и по формуле:
(2.24)
где А – суммарные мольные доли СО2 и H2S в газе; В – мольная доля H2S.
Рисунок 2.11 – Зависимость псевдокритической температурной поправки ε от концентрации в смеси СО2 и фактора ацентричности ω.
Зная Рпк, Тпк и ω вычисляют новые псевдокритические параметры:


Рисунок 2.12 – Зависимость псевдокритической температурной поправки ε от концентрации в смеси СО2 и H2S.
Зная Рпк, Тпк и ω, вычисляют новые псевдокритические параметры:
По известным величинам заданных Р и Т и вычисленным Р * пк и Т * пк рассчитывают приведенные параметры:


Используя графики, приведенные в [18] определяют Z (0) и Z (1) , а затем, используя формулу (2.21), вычисляют значение Z.
При наличии в газе СО2 и H2S коэффициент сверхсжимаемости Z определяется аналогичным образом, с той лишь разницей, что при вычислении фактора ацентричности ωугл по формуле (2.23) из состава газа исключается не только СО2, но и H2S.
Если для определения газов, содержащих кислые компоненты, т.е. СО2 и H2S, используются графики, показанные на рисунках 2.1 и 2.2, то последовательность расчета выполняется следующим образом:
– по формулам (2.3) рассчитываются значения Рпк и Тпк;
– по графикам из рисунка 2.11 находят поправочный коэффициент ε;
– вычисляются новые псевдокритические параметры по формулам
(2.27)
где xH2S – мольная доля сероводорода в смеси;
(2.28)
Используя формулу (2.26), рассчитывают величины Рпр и Тпр, а затем по этим приведенным параметрам из графика в [18] находят коэффициенты сверхсжимаемости Z (0) и Z (1) . По известным Z (0) и Z (1) вычисляют Z.
Для более точных расчетов коэффициент сверхсжимаемости природных газов Z должен быть определен по кубическим уравнениям состояния газов, наиболее широкое распространение, среди которых получили уравнения Соаве, Редлиха-Квонга, Пенга-Робинсона. При этих методах расчета присутствие в газе кислых компонентов практически не влияет на величину погрешности при определении Z, если расчеты ведутся с учетом коэффициентов взаимодействия.
Для определения коэффициента сверхсжимаемости Z кубические уравнения состояния решаются относительно Z. Имеющее достаточно высокую точность уравнение Редлиха-Квонга для определения Z записывается в виде:
(2.29)


Уравнение (2.29) дает искомую точность для газообразных компонентов и их смесей. Наличие в смеси компонентов в жидком состоянии, а также молекул различного строения резко увеличивает погрешность расчетов.
Повышение точности величины Z при этом возможно путем введения поправки ΔZ на Z, определенной по формуле (2.21).
Наиболее точно коэффициент сверхсжимаемости Z определяется из уравнения состояния Пенга-Робинсона, имеющего относительно Z вид:
См. ниже за таблицей 2.5:
Z 3 –(l–A)Z 2 +(A–3B 2 –2B)Z–(AB–B 2 –B 3 )=0, (2.32)
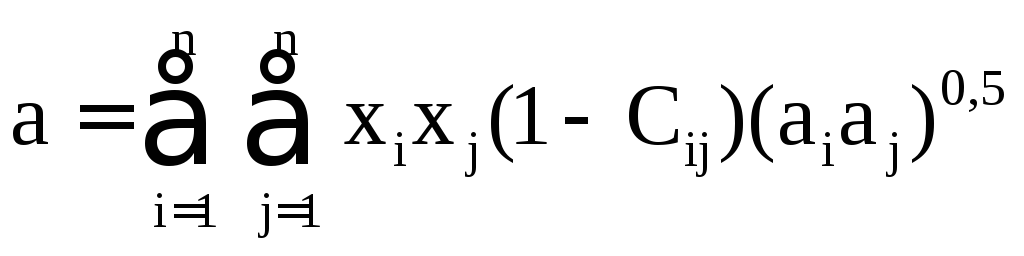





Значения коэффициента Cij в формуле (2.34) приведены в таблице 2.5.
Таблица 2.5 – Значение коэффициента Сij в формуле (2.34)
Источник
2.5.2 Определение коэффициента сверхсжимаемости по двум параметрам
Методика определения коэффициента сверхсжимаемости газа по двум параметрам, является наиболее простой, и заключается в графическом определении Z по двум приведенным параметрам Рпр.см и Тпр.см. Эту методику можно использовать, когда природные газы содержат не более 2 % мольных высококипящих углеводородов С5+.
Порядок определения Z следующий:
1) По формулам 2.10 и 2.11 находят критические параметры газовой смеси (Ркр и Ткр);
2) По формулам 2.12 рассчитывают приведенные параметры газовой смеси (Рпр.см и Тпр.см);
3) По графику Стендинга-Катца представленному на рисунке 2.7 определяют для рассчитанных Рпр.см и Тпр.см коэффициент сверсжимаемости газа Z.
Рисунок 2.7 – Графическая зависимость Стендинга-Катца для определения коэффициента сверхсжимаемости природного газа Z
2.5.3 Коэффициент расширения газа
В практике разработки месторождений используется уравнение состояния реальных газов (2.9) для определения соотношений между объемами углеводородов в пластовых и поверхностных условиях. Для реального газа это соотношение выражается через коэффициент расширения газа или объемный коэффициент газа.
Коэффициент расширения газа Е – это безразмерный параметр, показывающий во сколько раз объем газа при стандартных условиях Vcт (Ратм=101325 Па и Тст=293 К) больше объема, который занимает этот газ в пластовых условиях Vпл.
Используя уравнение состояния реального газа (2.9), для стандартных условий (Ратм=101325 Па, Тст=293 К, Zcт=1), коэффициент расширения газа Е можно представить следующим образом:
Коэффициент расширения газа используется при подсчете запасов газовых месторождений приведенных к стандартным условиям. Для этого используется следующее уравнение:
где Ен.д – коэффициент расширения газа при начальном давлении и температуре на приведенной глубине залежи, которая соответствует горизонтальному сечению пласта, делящему массу газа, содержащемуся в этом пласте, пополам; Vг.з.г – геологические запасы газа в залежи, приведенные к стандартным условиям на поверхности Земли, м 3 ; Vг.ч.з – объем газонасыщенной части залежи, м 3 ; mот – коэффициент открытой пористости, доли единиц; Sв – коэффициент остаточной водонасыщенности, доли единиц.
2.5.4 Плотность природного газа
Используя уравнение состояния реального газа (2.9), можно рассчитать плотность и относительную плотность природного газа по воздуху.
Плотность природного газа. Плотность – это отношение массы вещества к его объему, является одним из основных параметров характеризующих газ, в системе СИ измеряется кг/м 3 . Величина, обратная плотности, называется удельным объемом.
У равнение состояния реального газа
Источник